[Artificial Intelligence] 특징을 추출하는 합성곱 신경망의 기초

Chance약 2 분

📷 합성곱 신경망(Convolution Neural Network)

합성곱 신경망(Convolution Neural Network)은 합성곱을 이용한 신경망으로
이미지 처리 분야에서 공간에 대한 특징 추출에 유리하여 많이 사용되는 형태입니다.

이를 이용하여 신호 처리, 이미지 특징 분석, 컴퓨터 비전 등에서 사용됩니다.

🔢 특징 맵(Feature Map)?

특징 맵(Feature Map)은 데이터가 커널(Kernel)이라는 필터(Filter)를 거치며,
선형 결합을 통해 계산된 결과를 반환한 표 정도로 생각하는 것이 좋다고 생각됩니다.

여기서 선형 결합이란 커널을 이용하여 데이터의 요소를 곱한 값을 더하는 것입니다.

1️⃣ 1차원 데이터

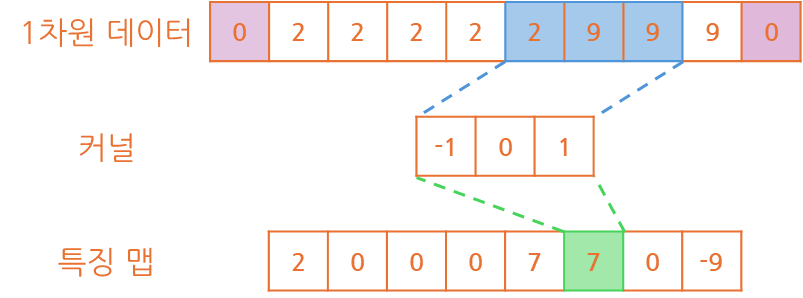
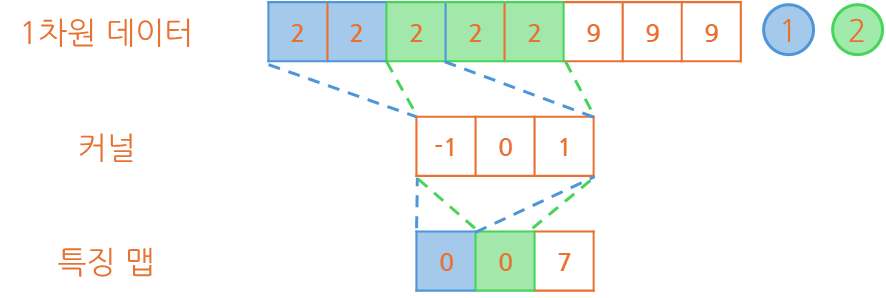
예를 들어 1x8 크기의 1차원 데이터를 1x3 크기의 커널을 이용해 계산해볼 경우
아래와 같이 연산이 수행되어 1x6 크기의 특징 맵을 반환하는 것이 확인됩니다.

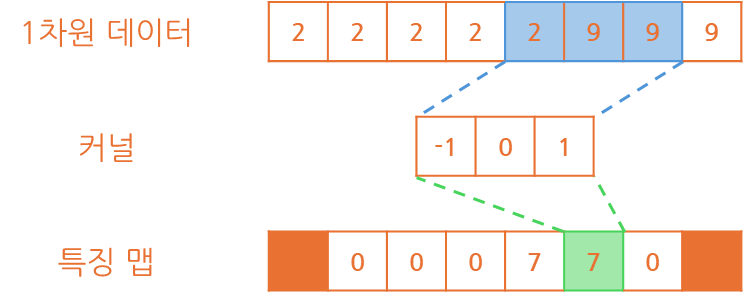
알 수 있는 것은 커널 크기가 1x3이라면 특징 맵의 크기가 2개 줄었다는 것과
특징 맵은 1x3인 경우 (-1, 0, 1) 데이터로 이뤄져서 만들어지는 것이 파악됩니다.

규칙으로 인지하신 분도 있겠지만 커널은 0을 기준으로 값의 대칭을 이루고 있으며,
이 값의 대칭을 이루기 위해 커널의 크기는 3, 5, 7과 같은 홀수로 구성되고 있습니다.

1차원 데이터를 커널을 통해 특징 맵을 도출하는 수식은 아래와 같이 구성됩니다.

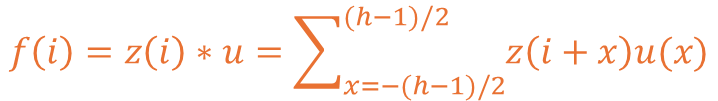
여기서 z는 입력된 데이터를 u는 커널을, 마지막으로 h는 커널의 크기입니다.
수식에 표에서 제공된 3이라는 커널의 크기를 대입하여 계산해보도록 하겠습니다.

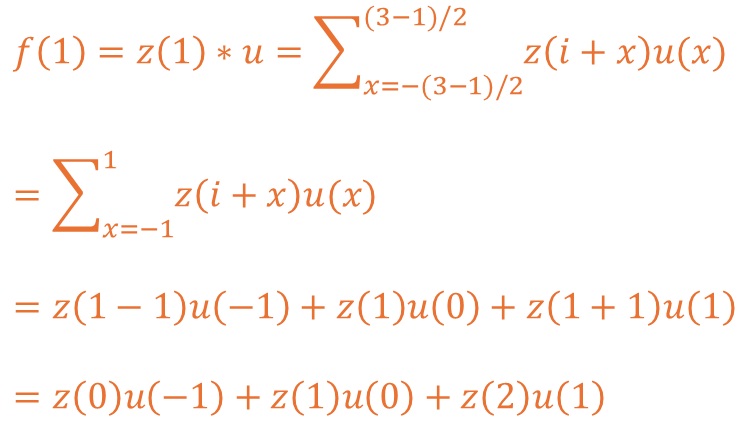
f가 1인 경우 0번, 1번, 2번에 각각 -1, 0, 1을 곱한 뒤 더하는 것이 확인됩니다.
이렇게 될 시 f가 0이거나 예제 기준 7인 경우 계산이 성립되지 않는게 확인됩니다.

2️⃣ 2차원 데이터

1차원 데이터에 대한 구조를 이해했다면 2차원 데이터에 대해서도 확인해보겠습니다.

2차원 데이터는 8x8 형태이고 커널의 크기도 2차원의 형태로 3x3 크기로 구성하였습니다.

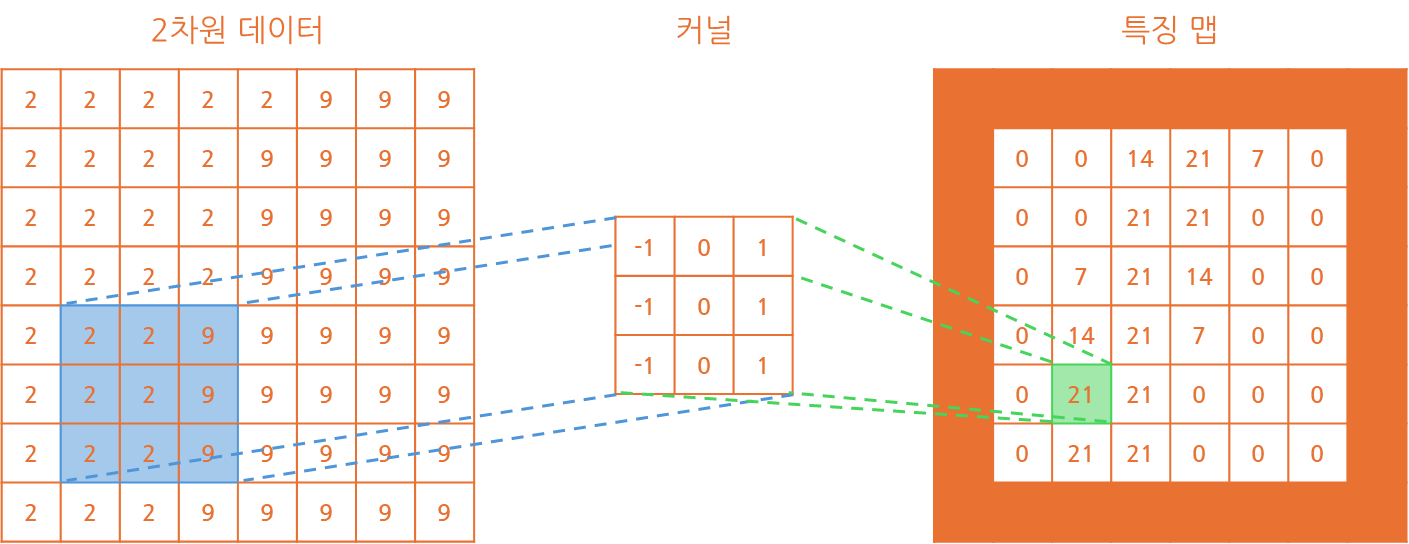
마찬가지로 확인 가능한 것은 특징 맵의 크기가 기존 데이터에 비해 작아졌다는 것과
커널이 이전과 비슷하게 ((-1, 0, 1), (-1, 0, 1), (-1, 0, 1)) 형태로 생성됐다는 것입니다.

그렇다면 이러한 형태의 커널을 적용하는 수식은 어떻게 구성되는지 살펴보겠습니다.

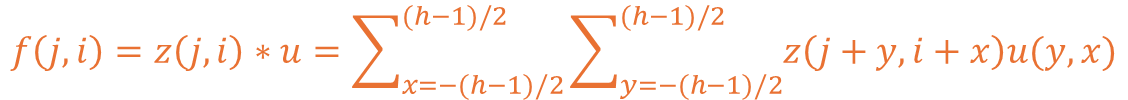
기존 1차원 데이터에서 크게 변화하지는 않았고 수식에 추가만 된 형태가 확인됩니다.
기존에는 x 축만 이용했기에 x만 있었지만 이제는 y 축의 값도 이용하고 있습니다.

해당 수식에 마찬가지로 커널의 크기인 h 값에 3을 대입하여 확인해보도록 하겠습니다.

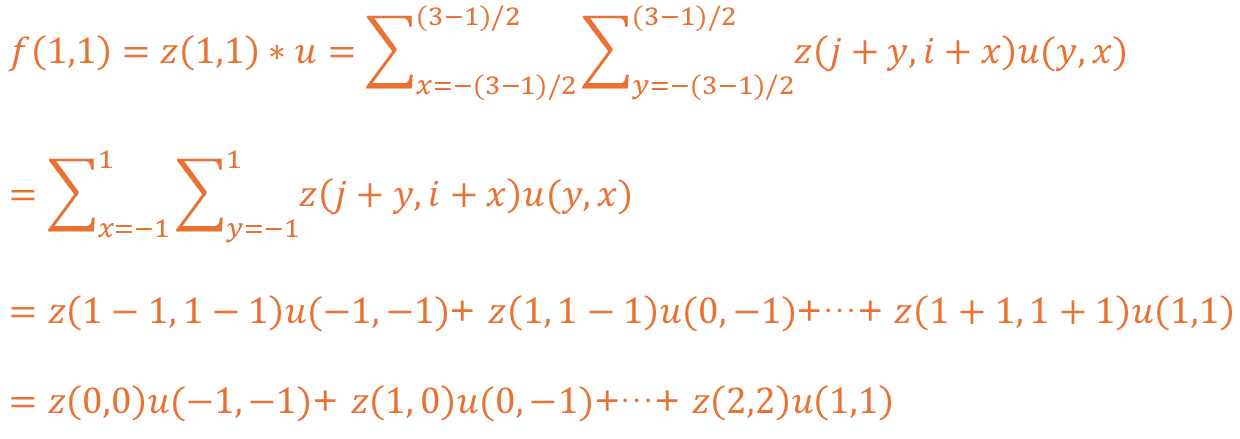
추가로 제가 표현한 커널의 경우 오른쪽 값에서 왼쪽 값을 빼는 형태를 띄고 있습니다.
해당 형태를 수직 엣지 라고 표현하고 이는 수직 데이터에 대한 특성을 추출합니다.

만약 흑백의 밝기를 이용하여 추출할 경우 오른쪽이 밝은 경우 값이 양수로 표현될 것이고,
반대로 왼쪽이 밝거나 오른쪽이 비교적 어두운 경우 값이 작기 때문에 음수로 표현됩니다.

그렇기에 수평 형태 추출이 필요하고 위 값에서 아래 값을 빼는 형태를 만들 수 있습니다.
이 경우 수평 엣지의 커널은 ((1, 1, 1), (0, 0, 0), (-1, -1, -1)) 형태를 띄는 걸 알 수 있습니다.

이런 형태를 이용해 이미지의 경우 색상 영역의 RGB를 포함한 다양한 특성을 추출합니다.

물론 이러한 커널도 하나의 가중치이므로 신경망의 학습 과정에서 값이 조정되게 됩니다.

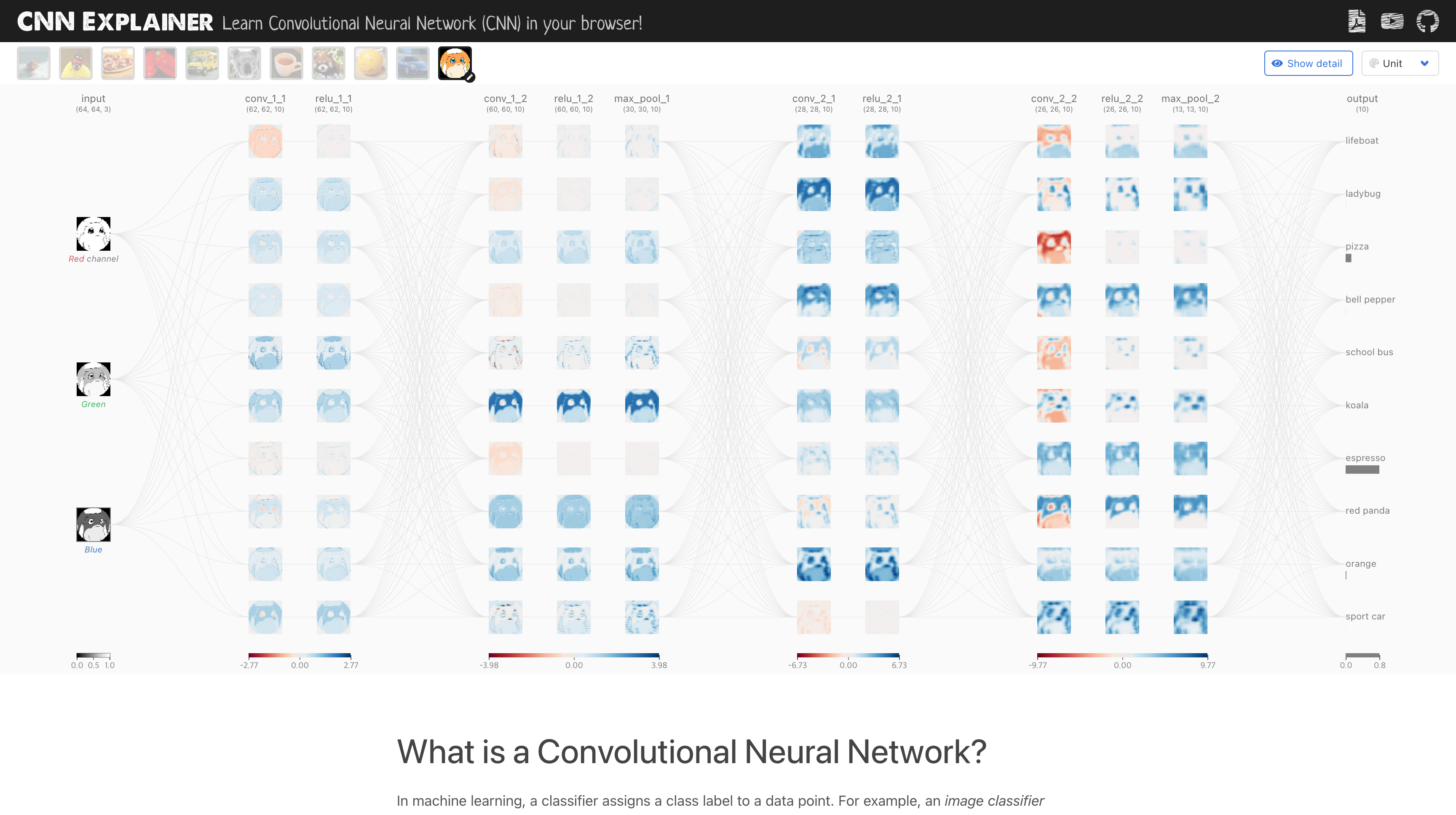
CNN Explainer 페이지를 통해 합성곱 신경망에서 커널에 따른 특징 맵 확인이 가능합니다.

🖼️ 합성곱 층(Convolution Layer)

위에 설명한 특징맵을 추출하기 위한 과정이 합성곱 층(Convolution Layer)의 역할입니다.

합성곱 층에서는 출력 데이터를 유지하거나 축소, 그리고 바이어스 값을 주기도 합니다.
이번 파트에서는 각 방법에 대해서 하나하나 알아보고 계산 방법도 알아보도록 하겠습니다.

💾 패딩(Padding)

커널의 구조 상 커널의 크기에 따라 특징 맵의 크기가 줄어든 것을 알 수 있습니다.

데이터의 입력이 부족한 결과로 (h - 1) / 2개만큼 각 축에 특징 맵을 축소시키게 됩니다.
하지만, 커널의 크기나 구성에 따라 특징 맵의 크기가 줄어들면 안되는 경우가 생기기도 합니다.

이런 상황에서 사용 가능한 것이 마치 입력이 더 커보이게 하는 패딩(Padding)이라는 방법입니다.

방법으로는 별도의 패딩을 적용하지 않아 특징 맵의 크기가 줄어드는 유효(Vaild) 패딩과
입력 데이터의 크기와 특징 맵의 크기가 동일하게 유지되는 동일(Same) 패딩으로 나뉩니다.

상위 방식에 대해서는 별도의 설명은 하지 않으며, 채울 때의 방식 두 가지를 소개드리겠습니다.

🫗 0 패딩(Zero Padding)

0 패딩(Zero Padding)은 부족한 데이터를 0으로 채우는 방법이라 볼 수 있습니다.
해당 방식은 0을 추가하므로 추가된 데이터의 영향이 적어 일반적으로 많이 사용됩니다.

패딩의 크기는 p라 표현되고 1차원 데이터에 p의 값을 1로 설정하면 아래와 같습니다.

p의 크기를 1로 설정했지만 양쪽에 데이터가 1개씩 추가된 것을 확인할 수 있습니다.
2차원 데이터는 p의 값을 1로 설정할 경우 아래와 같은 형식으로 반영될 것입니다.

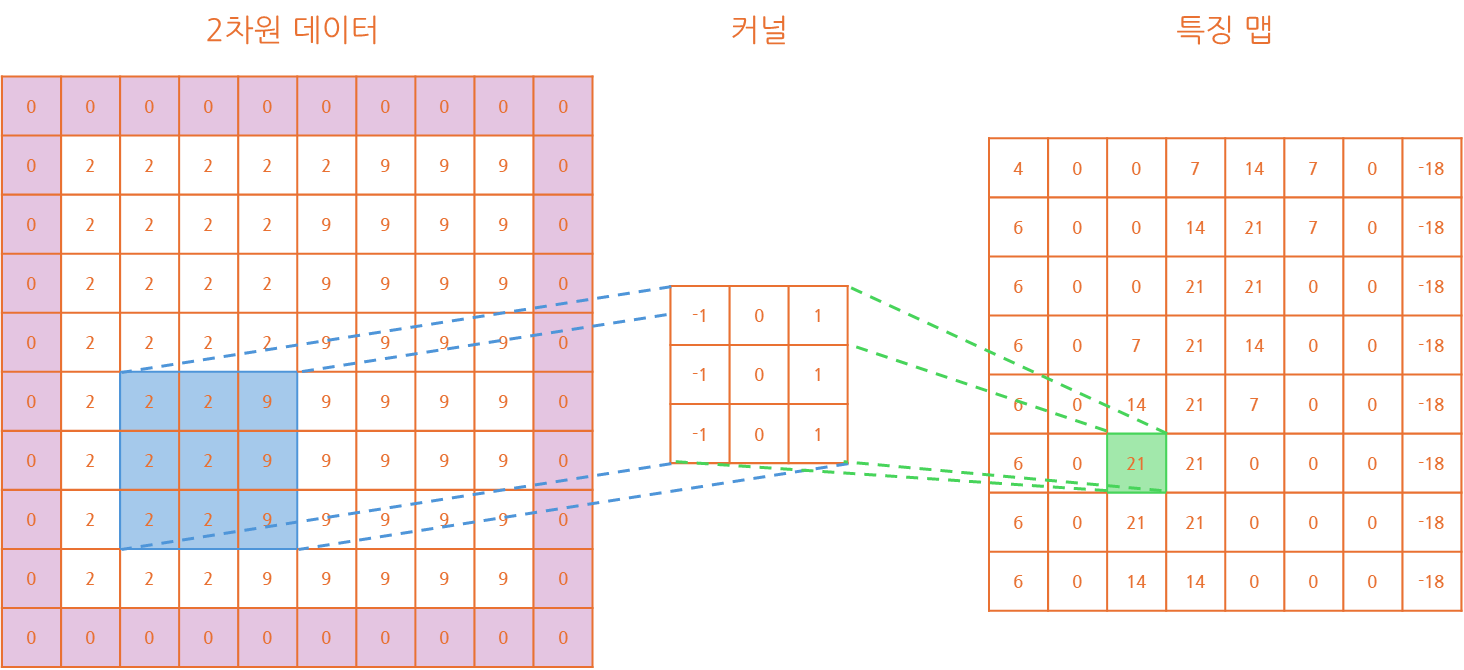
2차원이라는 특징에 따라 상하좌우 모두 데이터가 1개씩 추가된 것을 확인할 수 있습니다.

🖨️ 복사 패딩(Copy Padding)

복사 패딩(Copy Padding)은 근접한 데이터를 복사하는 형식으로 사용되는 방식입니다.

1차원 데이터를 기준으로 복사 패딩을 적용할 경우 아래와 같이 수행될 수 있습니다.

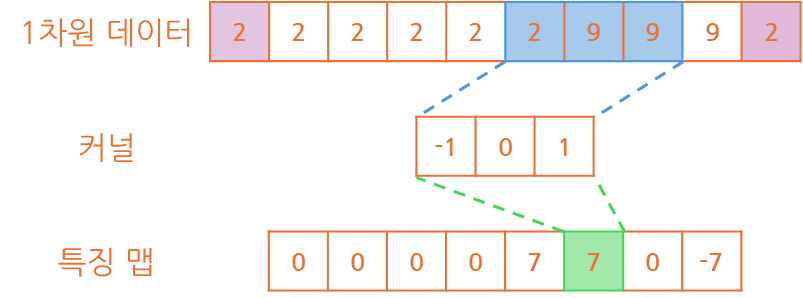
아무래도 데이터가 복사되어 적용됐기 때문에 해당 값을 보존하는데 좋은 방법입니다.
만약 2차원 데이터에 적용할 경우 아래와 같이 적용되는 것을 확인하실 수 있습니다.

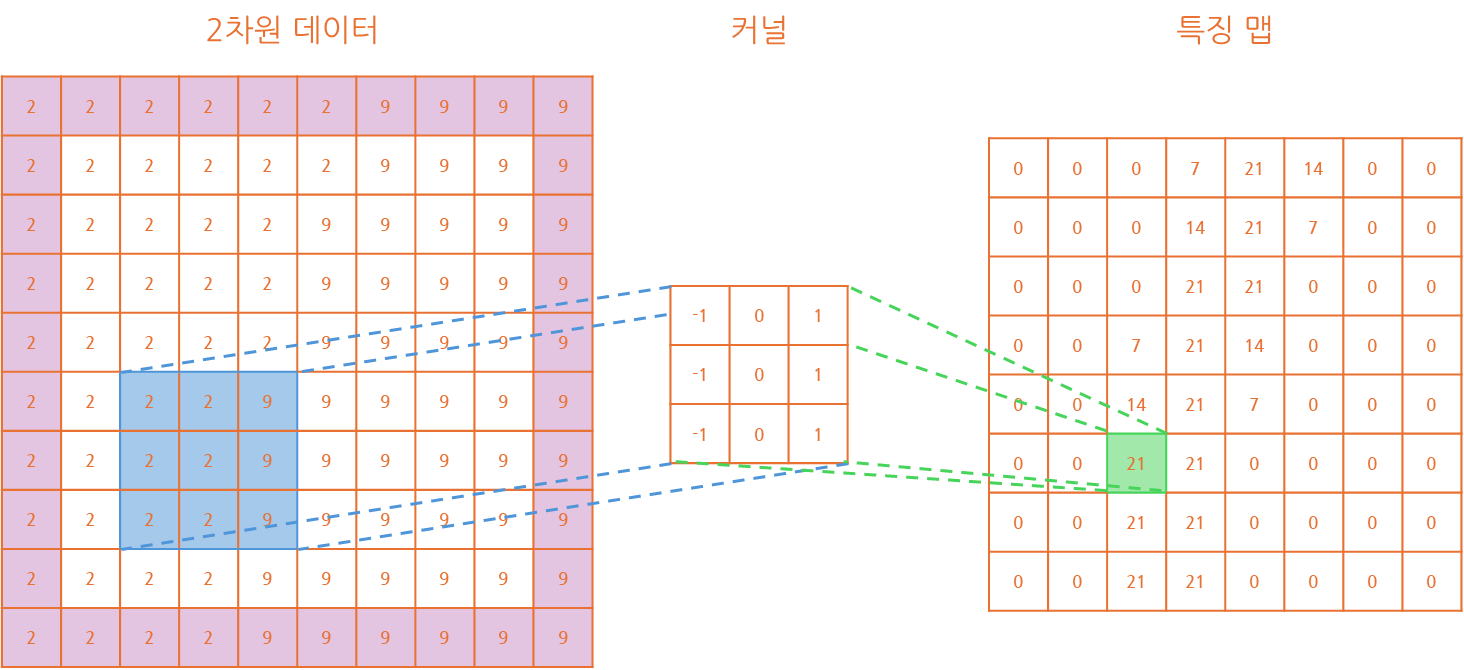
기존 0 패딩과 달리 값들이 기존의 특징을 조금 더 갖고 있는 것이 확인됩니다.

✂️ 스트라이드(Stride)

스트라이드(Stride)는 데이터에 커널을 적용할 때 이동거리를 의미한다고 볼 수 있습니다.

기본적으로 스트라이드는 s라는 값으로 표현하고 기본 상태의 경우 1의 값을 갖고 있습니다.
1의 값을 갖는 경우 1칸씩 오른쪽으로 이동하는 것을 의미하고 이를 통해 특징 맵이 추출됩니다.

1인 상태에서 이동 형태를 그림으로 표현하면 아래와 같이 이동된다는 것을 알 수 있을 겁니다.

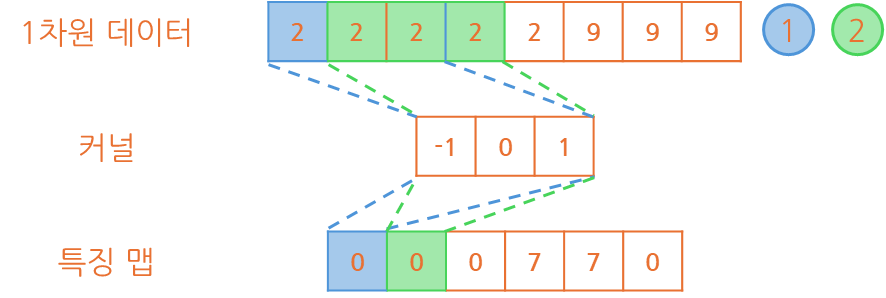
이동할 때 한 칸씩 옆으로 이동하여 커널을 적용하고 특징 맵을 만들고 있는게 보입니다.
그렇다면 스트라이드 값을 2를 준다면 어떻게 될지 그림으로 한 번 살펴보겠습니다.

스트라이드를 적용했더니 한 칸씩 이동하던 것이 두 칸씩 이동하는 효과가 적용됐습니다.
이를 통해 기존 한 칸씩 이동하던 것에 비해 1/2로 특징 맵이 줄어든 것이 확인됩니다.

스트라이드는 결국 s의 크기만큼 특징 맵의 최종 크기를 1/s로 만들게 됩니다.
해당 개념은 이후 설명될 풀링 층의 개념에서도 사용되오니 참고 바랍니다.

➕ 바이어스(Bias)

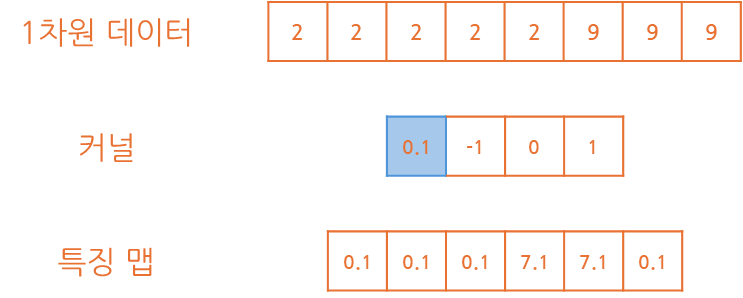
바이어스는 각 커널을 통과할 때의 기본적인 가중값을 제공하는 것을 의미합니다.
그림으로 표현하면 아래와 같이 커널 통과 시 값이 그만큼 추가된 것이 확인됩니다.

📚 커널의 크기

커널의 크기는 h로 표현하고 있고 2차원 데이터는 h*h 크기의 커널이 사용됩니다.

또한 커널은 입력 데이터의 면 그러니 특징 맵의 채널만큼 생성이 필요하게 됩니다.
예를 들어 RGB 형태의 데이터를 입력 값으로 제공한 경우 아래와 같이 구성될 것입니다.

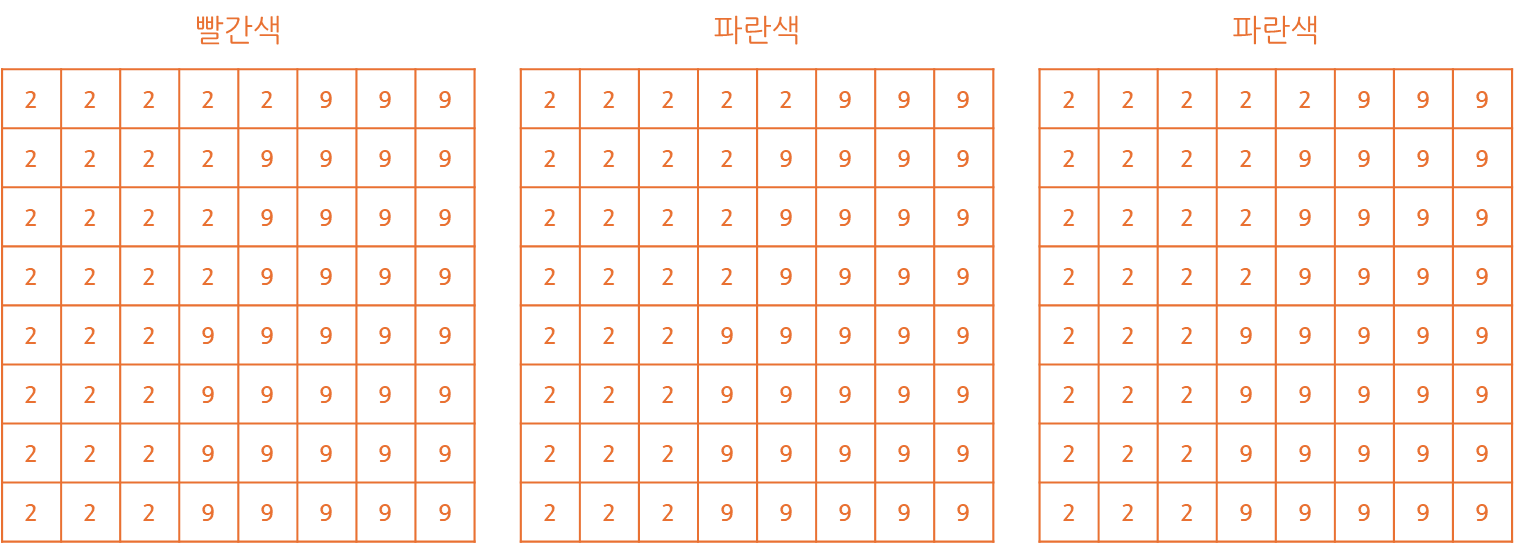
위와 같이 R, G, B는 3개의 채널이 합쳐져 하나의 그림을 구성하는 형태로 볼 수 있습니다.
이미지가 실제 의미하는 바를 파악하려면 3개의 채널에 특징 맵을 추출해야할 것입니다.

그렇다면 기본적으로 커널은 h*h의 크기로 구성되지만 앞서 제공된 데이터의 채널만큼
단일 커널의 크기가 결정되고 커널 크기는 h*h*k(입력 데이터의 채널)로 구성됩니다.

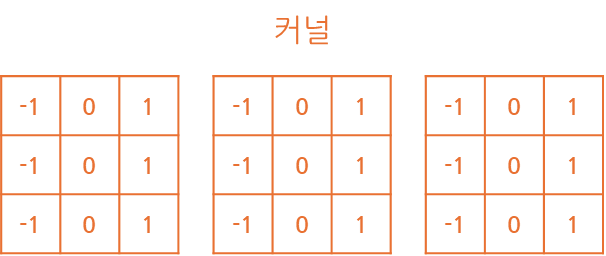
여기서 알 수 있는건 입력 데이터, 앞 층의 특징 맵이 여러 채널이란 걸 파악할 수 있습니다.

특징 맵이 여러 장이란 것은 앞 층에서 여러 개의 커널을 갖고 있다는 것을 의미하게 되며,
이러한 커널의 개수는 k라는 형식으로 표현하고 현재 층의 개수를 k'로 표현하게 됩니다.

k'의 개수는 다음 합성곱 층의 단일 커널의 채널과 동일하다는 것을 알 수 있습니다.

#️⃣ 계산 방법

위와 같이 패딩, 스트라이드를 이용할 경우 특징 맵의 크기가 변경되는 것이 확인됩니다.
또한 커널의 크기 뿐만 아니라 개수도 중요한 역할을 하고 있기에 명확한 계산이 필요합니다.

간단하게 여기서 한 가지 예시를 통해 계산하는 방법을 파악하고 특징 맵의 크기를 보겠습니다.

파라미터
- 입력 데이터 (x*y*k): 512 * 512 * 3
- 커널 개수 (k'): 128
- 커널 크기 (h): 5
- 패딩 (p): 1
- 스트라이드 (s): 2
결과
- 커널 크기: 5 * 5 * 3
- 특징 맵 크기
  - 패딩 적용: (512 + (1*2)) * (512 + (1*2)) = 514 * 514
  - 커널 통과: 514 - ((5-1) / 2 * 2) * 514 - ((5-1) / 2 * 2) = 510 * 510
  - 스트라이드 적용: (510 / 2) * (510 / 2) = 255 * 255
  - 커널 개수 적용: 255 * 255 * 128
- 가중치 개수: 5 * 5 * 3 * 128 = 9,600개

상위 내용은 간단하게 기존의 계산 방식을 이용하여 현재 층의 특징 맵을 예상한 값입니다.
이러한 계산 방식을 이용하면 다음 입력 데이터를 예상하여 합성곱 층을 구성 가능합니다.

⏭️ 풀링 층(Pooling Layer)

합성곱 층 이후에 위치하는 층으로 특징 맵에 지나친 상세함을 줄이는 목적을 갖습니다.
동작 방식은 커널을 거칠 때 값을 요약하고 이를 특징 맵에 반영하여 생성하는 형태입니다.

이전 설명한 스트라이드를 이용해 커널 크기에 맞춰 특징 맵의 크기를 줄이는 형식으로
이렇게 진행 시 특징 맵의 크기를 줄여 이미지를 다운샘플링하는 것과 같은 효과를 보입니다.

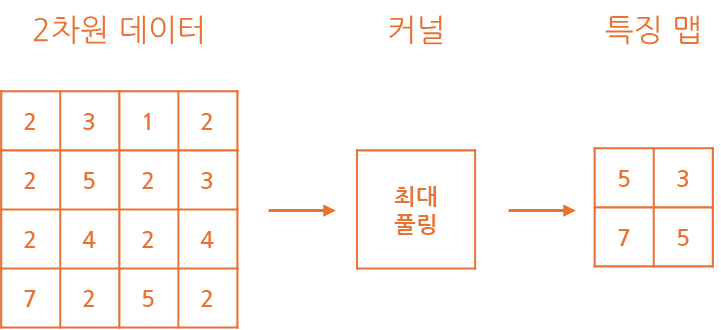
일반적인 풀링 방식으로는 풀링 커널 내 가장 큰 값을 남기는 최대 풀링 방식과
풀링 커널 내 값의 평균 값을 연산하여 남기게 되는 평균 풀링 방식이 사용됩니다.

합성곱 층과의 차이는 커널에 별도의 가중치가 존재하지 않다라는 점이 존재하고,
말 그대로 요약을 위한 층이기 때문에 채널의 크기에도 변동을 주지 않게 됩니다.

💫 특징

최종 특징으로는 부분 연결성과 가중치 공유라는 특성이 있다는 것을 확인할 수 있습니다.

기존 알고리즘들은 완전 연결성의 특징에 따라 입력 노드가 은닉 노드와 모두 연결됩니다.
이러한 완전 연결성의 특징에 따라 각 노드 별 가중치를 별도로 만들어 관리하고 있습니다.

하지만 합성곱 신경망은 확인 시 커널이라는 가중치를 공유해서 사용한다는게 확인됩니다.
또한 커널은 모든 데이터, 즉 노드와 연결되지 않기에 부분 연결성의 특징을 갖습니다.

이러한 특성을 이용하여 가중치 갱신에 소요되는 시간을 줄일 수 있다는 장점을 보여줍니다.

다음 포스팅에서는 합성곱 신경망의 주요적인 구조와 예시를 알아보겠습니다.

정말 긴 글 끝까지 읽어주셔서 감사드립니다. 😎