[Artificial Intelligence] LeNet-5을 통해 알아보는 합성곱 신경망

Chance1분 미만

📚 합성곱 신경망의 구조

이전 포스팅에서는 합성곱 신경망을 구성하기 위한 기초 사항에 대해서 알아보았습니다.

합성곱 신경망도 마찬가지로 깊은 신경망으로 구성하고 있어 구조 파악이 필요합니다.
만약 여러 층으로 구성된다면 각 층의 특징 맵의 크기와 채널을 미리 파악해야 합니다.

마치 빌딩 블록처럼 신경망을 쌓아가고 어떠한 형식으로 쌓아가는지 확인해보겠습니다.

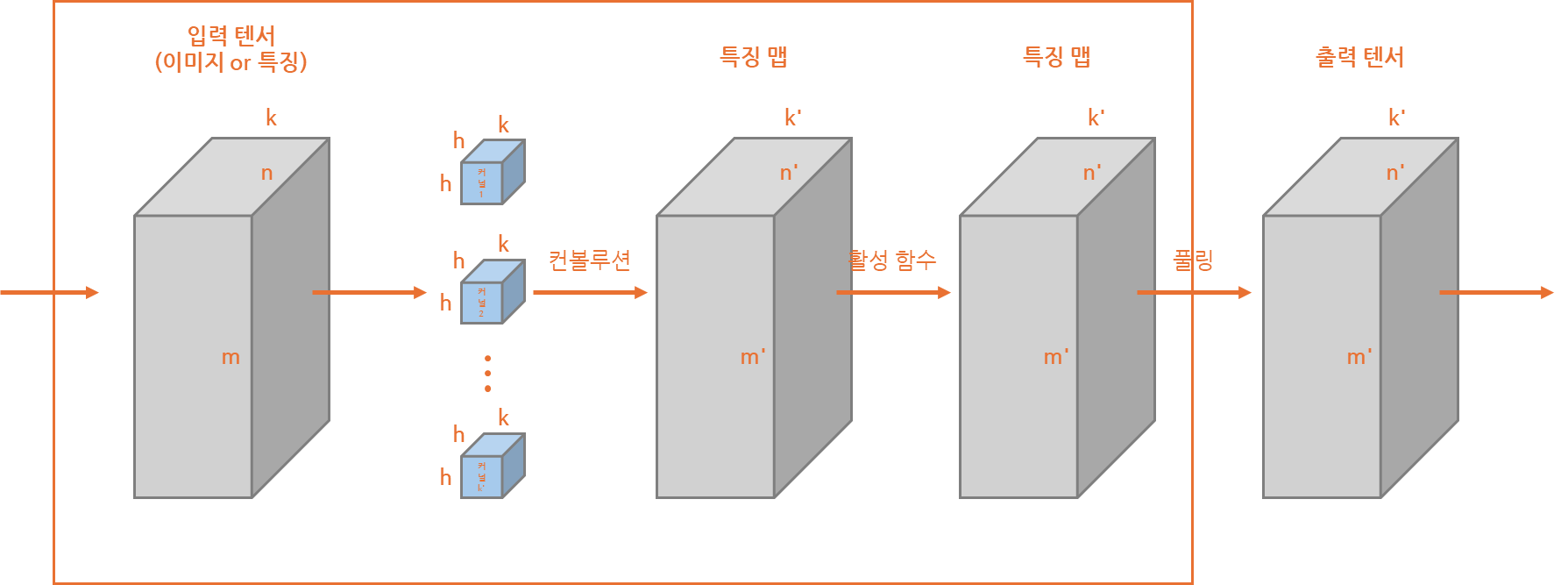
합성곱 신경망은 위와 같이 간단하게 쌓아놓은 예제로 상위와 같이 구성될 수 있습니다.
해당 구성은 간단한 표현을 위한 구성도이나 확인해보면 일정한 특징 확인이 가능합니다.

우선 단일 커널의 면의 수, 즉 채널은 입력 텐서(데이터)의 채널과 동일하다는 것과
커널의 개수(k')가 다음 층의 특징 맵의 채널과 동일하다는 것이 확인되고 있습니다.

이런 특징은 합성곱 신경망에서 지속 사용되는 개념이니 미리 이해하는 것이 좋습니다.

합성곱 신경망의 구조를 이용하여 필기 숫자인식 문제에서 입증한 알고리즘입니다.

해당 알고리즘은 지금의 합성곱 신경망을 이용하는 방식에 비해 단순한 구조이지만,
합성곱 신경망의 기본적인 구조를 이해하는데 도움이 될 것이라 생각하여 소개합니다.

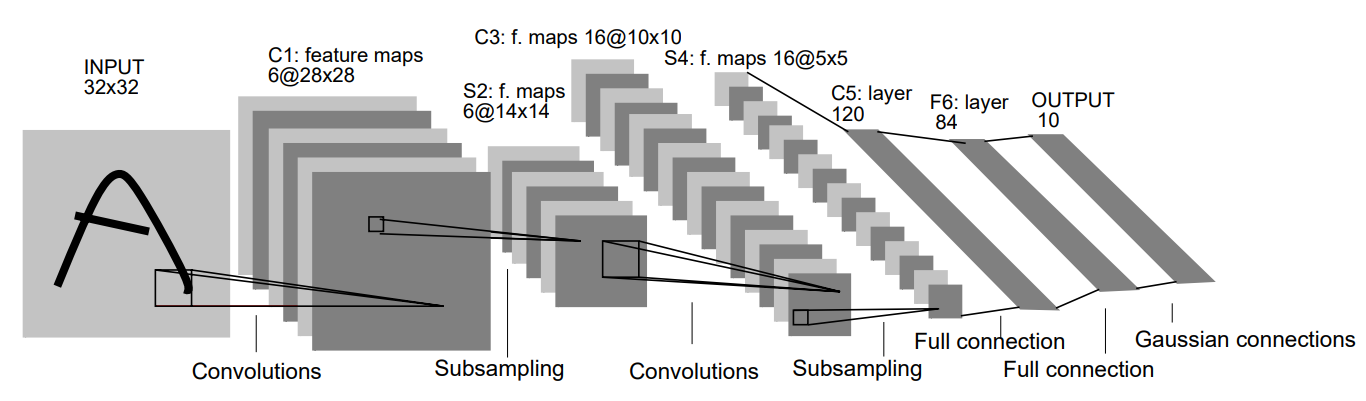
첨부해놓은 그림은 LeNet-5가 공개된 LeCun1998이라는 논문의 첨부된 그림입니다.

해당 그림에서는 Convolutions(합성곱) 과정과 Subsampling로 표현된 풀링 과정,
Full connection인 완전연결층, 결과 출력의 Gaussian connections가 있습니다.

각 층을 지나면서 이미지에 대한 데이터 크기와 채널의 변경점을 표현하고 있지만,
이를 조금 더 보완하여 각 층마다 어떠한 파라미터를 갖고 있는지 알아보겠습니다.

각 합성곱 층과 풀링 층에서 파라미터와 마지막에 Flat해진 것이 확인되고 있습니다.
이렇게 Flat해진 데이터를 완전연결층을 통해 점차 줄이고 10개의 출력으로 축소됩니다.

Flat의 과정을 Flatten이라고 표현하며 완전연결층에서의 가중치를 줄이기 위해서
최근에는 전역 평균 풀링을 층으로 만들어 Flatten 과정을 수행하기도 하고 있습니다.

이러한 과정에서 사용된 가중치의 개수를 계산할 수 있는데 아래와 같이 계산되게 됩니다.

가중치 개수
- 합성곱 층: (5*5*1+1)*6 + (5*5*6+1)*16 + (5*5*16+1)*120 = 50,692 개
- 완전연결층: (120+1)*84 + (84+1)*10 = 11,014 개
- 총합: 50,692 + 11,014 = 61,706 개

그렇다면 총 갱신해야하는 가중치의 개수는 61,706개라는 것을 확인할 수 있을 겁니다.

이전 MSE나 엔트로피와 같은 손실 함수와 경사하강법과 같은 최적화 함수의 개념이
동일하게 적용되며, 출력층에 노드는 softmax와 같은 함수로 결과를 표현하게 됩니다.

기존 완전연결층과 차이가 있다면 노드 간 연결되는 엣지에 대한 가중치를 갱신했다면
합성곱 신경망은 커널에 존재하는 공용으로 사용되는 가중치가 갱신된다는 것 입니다.

이렇게 된다면 각각의 데이터, 노드가 한 층에서는 같은 가중치를 공유하게 됩니다.
이를 통해 완전연결층의 노드 간 가중치에 비해 갱신이 필요한 가중치가 적어집니다.

기존의 컴퓨터 비전에서는 지난 포스팅에 표현과 같이 수직 엣지와 수평 엣지 등
구조를 사전 정의하고 파악 후 커널을 사람이 직접 설계해야하는 문제가 있었습니다.

현재는 딥러닝의 역전파 등의 가중치 갱신 방법을 이용하여 특징 추출을 진행 후
이를 분류까지 진행 후 돌아와 가중치를 갱신하는 형식을 이용하기 시작했습니다.

이렇게 된다면 특징 파악부터 분류까지 모두 한 번에 진행하는 것을 알 수 있으며,
특징을 학습한다는 특징 학습 또는 모두 진행의 의미로 통째 학습이라 표현합니다.

통째 학습
- 이전 소개한 것처럼 특징 추출부터 분류까지 모든 과정을 제공하고 있습니다.
특징 학습
- 특징 추출에 대한 알고리즘을 학습을 통해 파악하기에 성능 향상이 있습니다.
신경망의 깊이
- 가중치 공유를 이용하기 때문에 깊이가 깊어도 학습의 영향도가 적습니다.
- 소개한 LeNet-5 이후 신경망은 수십, 수백 층의 깊이로 구성하고 있습니다.
데이터 구조 유지
- 컬러 이미지의 경우 3차원 텐서로 합성곱 층 사용 시 3차원 텐서를 출력합니다.
- 다층 퍼셉트론의 경우 1차원 벡터 형태로 제공하고 있기에 정보 손실이 있습니다.
부분 연결성
- 기존의 다층 퍼셉트론은 완전 연결성의 특성으로 모든 노드가 엣지로 연결됩니다.
- 반면에 합성곱 신경망은 커널, 패딩, 스트라이드의 구조로 부분 연결성을 갖습니다.
가중치 공유
- 커널 구조를 이용하기에 가중치 공유 한 층에서의 가중치 갱신 대상이 적습니다.

다음은 합성곱 신경망 중 다른 신경망의 구조에 대해 알아보도록 하겠습니다.

끝까지 읽어주셔서 감사드립니다. 😎