[Artificial Intelligence] 경사하강법에 대해 알아보자

📉 경사하강법 (Gradient Descent)?

기계학습 간 최적화 함수의 대표 격인 경사하강법에 대해서 간단하게 소개하고자 합니다.

🦾 기계학습의 간단한 동작 과정

인공지능은 규칙 기반에서 기계학습을 이용한 데이터 기반까지 지속 발전 중에 있습니다.
기계학습에서는 기계가 주어진 데이터의 관계를 찾아 규칙을 만드는 것을 목적으로 합니다.

데이터의 관계를 찾는 과정에서 손실(실제 데이터와의 오차)이 최소인 값을 찾는 것이 목표로
손실은 손실 함수를 이용하여 오차를 계산하고 이를 보완할 값을 찾아 제공합니다.

보편적으로 손실 계산에서 가장 많이 사용하는 방식은 MSE(Mean Squared Error)입니다.
MSE는 직역 시 평균 제곱 오차로 오차의 제곱을 모두 더한 값의 평균을 의미합니다.

MSE를 수식으로 표현할 경우 아래와 같이 수식이 작성되는 것을 확인할 수 있습니다.
M은 전체 개수이며, ŷ는 실제 정답 값, y는 예측한 값을 의미하고 있습니다.

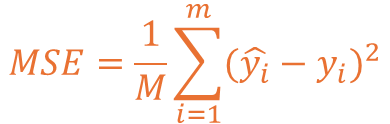
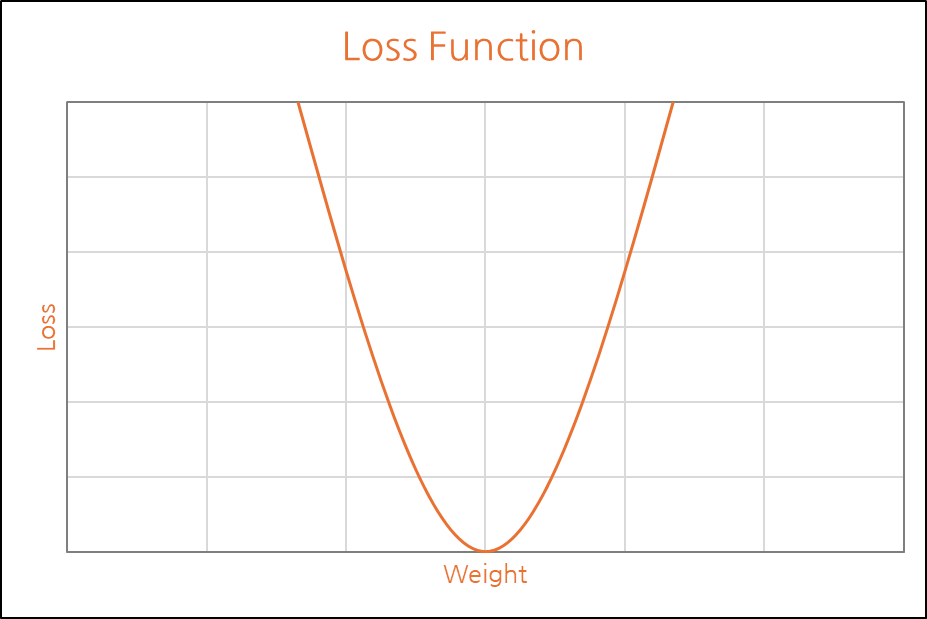
해당 기준의 손실함수를 그래프로 표현할 경우 아래와 같이 표현이 가능합니다.
우리가 찾아야할 값은 오차가 가장 최소가 되는 구간 임을 알 수 있습니다.

이러한 값을 가중치에 반영하여 최적화하는 과정에서 경사하강법을 사용하게 됩니다.

🤔 경사하강법의 동작 과정

그래프에서 보면 결국 가장 낮은 값, 즉 최소 오차를 찾아가는 것을 알 수 있습니다.
이러한 특성을 이용해 경사하강법은 그래프의 기울기에 따른 이동을 수행하게 됩니다.

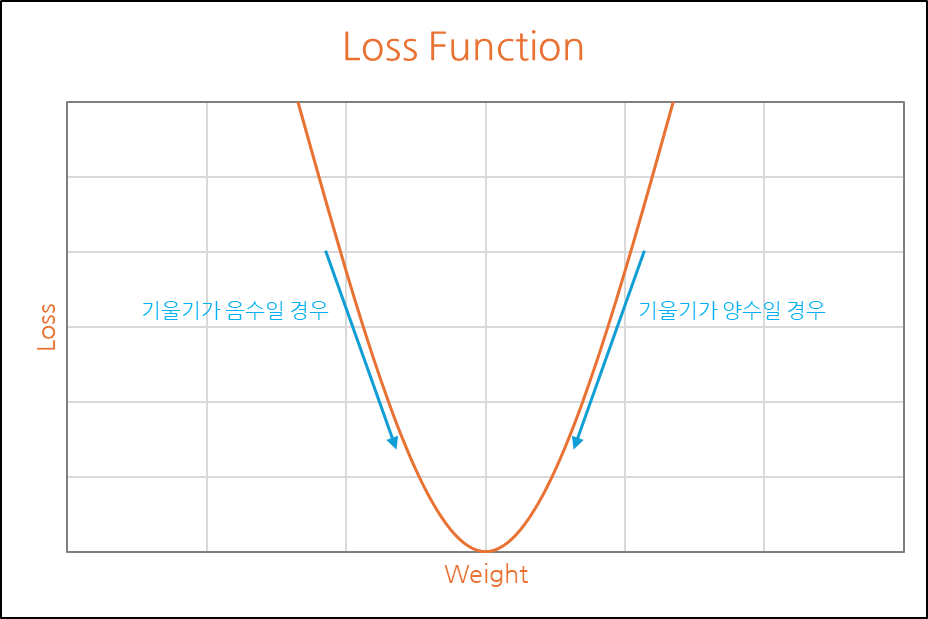
이러한 경사하강법의 학습 규칙을 수식 표현 시 아래와 같이 표현이 가능합니다.

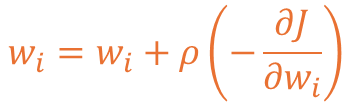
하나의 매개변수를 기반으로 손실함수 J를 wᵢ의 값으로 편미분한 값을 도출하고
𝜌(rho) 또는 p로 표현하는 학습률을 곱하여 값을 하강할 경사의 값을 조절한 뒤,
최종적으로 wᵢ 가중치 값의 오차를 반영하는 형태로 수식이 전개되고 있습니다.

📈 학습률 (Learning rate)

학습률은 오차 값을 기울기에 따라 반영 시 너무 크거나 낮은 값이 이동하는 것을 방지하기 위해
특정 값을 곱하여 학습 간 최적해 방향으로의 접근 값을 줄이는 행위를 의미하고 있습니다.

일반적으로 0.001, 0.0001과 같은 값이 쓰이며 해당 값을 찾는 것도 중요한 요소입니다.

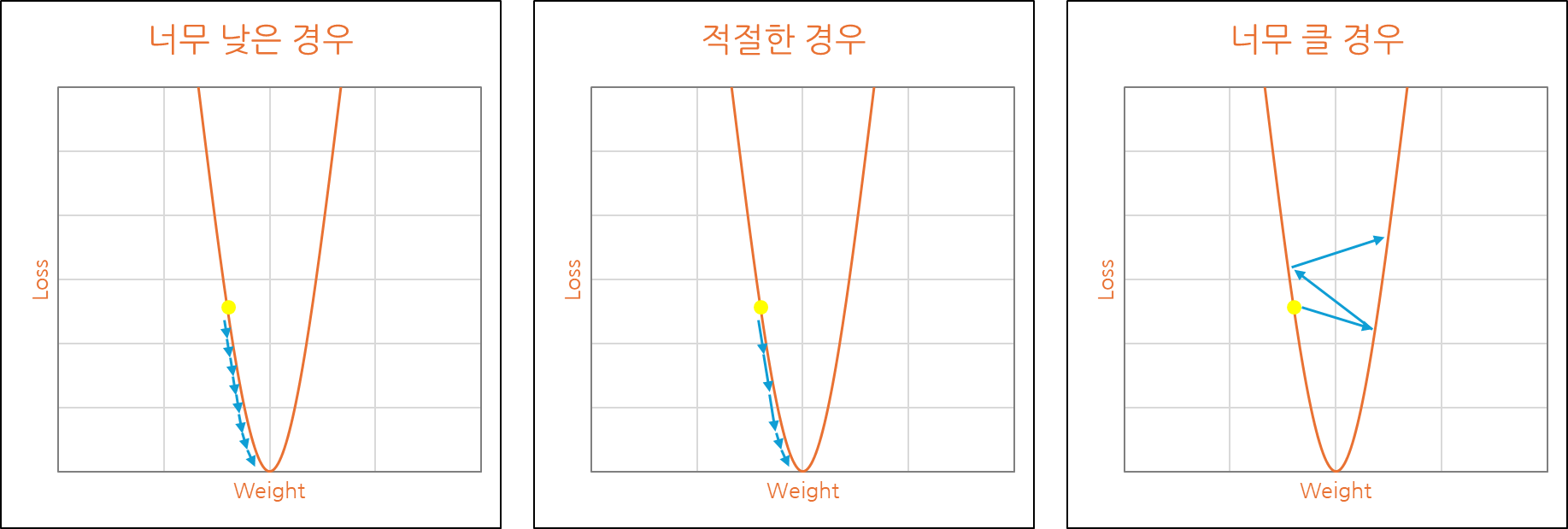
위 사진은 학습률 설정에 따른 최적해 방향으로의 이동 정도를 나타낸 것입니다.

너무 낮을 경우 학습 반영의 시간이 오래걸리고 Local Minimum에 빠질 수 있으며,
반대로 너무 클 경우 발산을 하여 정확한 값을 찾지 못하는 현상이 발생될 수 있습니다.

적절한 값을 찾을 경우 속도도 안정적으로 최적해에 도달하는 것을 볼 수 있습니다.

😅 경사하강법의 문제점

경사하강법은 기본적인 구조 상으로는 좋을 수 있지만 크나큰 문제가 있습니다.

위에서 언급된 Global Minimum이 아닌 Local Minimum을 찾을 수 있다는 점 때문입니다.

둘의 차이는 가장 지대가 낮은 구간을 찾았는지 찾지 못했는지의 차이로 볼 수 있으며,
Global Minimum은 가장 낮은 지대를, Local Minimum은 낮은 지대 중 하나를 의미합니다.

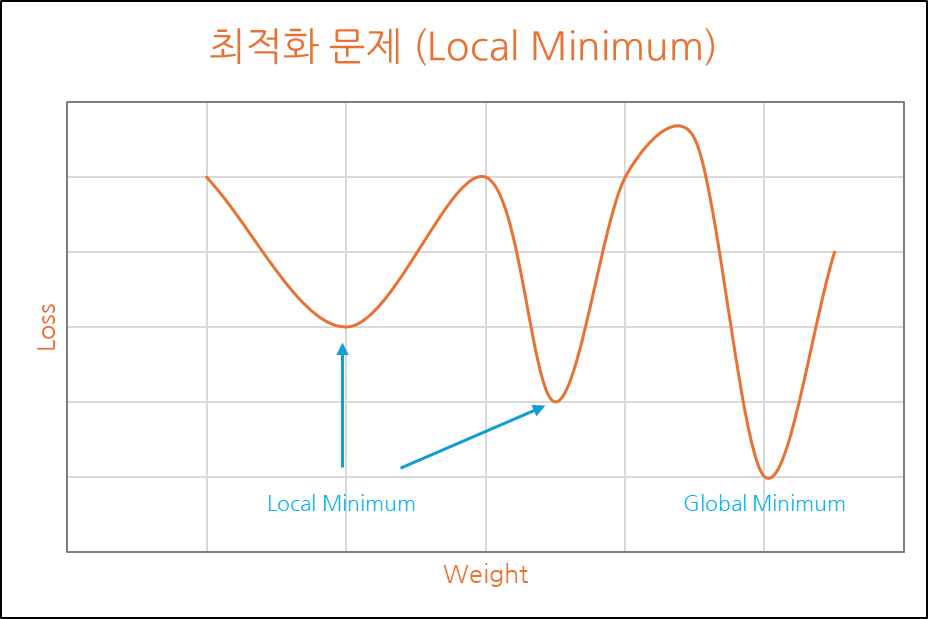
경사하강법의 기본 이론으로는 이를 극복하기 어렵기에 추가 고안된 다른 방법을 사용합니다.
다른 방법 중 Stochastic Gradient Descent 방법은 다음 포스팅을 통해 소개하겠습니다.

---

끝까지 읽어주셔서 감사드립니다. 😎