[Artificial Intelligence] 이전 가중치를 이용하는 모멘텀
⚽ 모멘텀(Momentum)은 무엇인가?
모멘텀(Momentum)은 물리학에서 사용되는 용어와 비슷한 개념이라고 보면 될 것 같습니다.
물리학에서는 운동량, 물체가 특정 이동하려고 하는 것을 의미하고 이는 관성이라 보면 됩니다.
🦾 모멘텀의 고안 이유
모멘텀은 기존 포스팅에서 설명드린 확률적 경사하강법(SGD)의 단점을 보완하기 위한 요소입니다.
기존의 SGD의 경우 가중치 갱신 과정에서 발산 등의 노이즈로 인해 속도가 느려질 수 있습니다.
속도 문제는 데이터의 차원과 양이 증가하면서 시간적인 부분과 정확성에 대한 문제가 생깁니다.
이러한 한계를 극복하기 위해 고안된 것이 모멘텀으로 위에서 설명한 관성의 원리를 이용하게 됩니다.
🤔 모멘텀의 동작 원리
관성을 생각해보면 이전에 발생한 운동량이 현재의 운동량에 영향을 끼치는 것이라 볼 수 있습니다.
모멘텀은 이전에 세대에서 갱신된 가중치와 방향을 이용하여 현재 세대에 일부 적용하는 것입니다.
그렇게 함으로써 SGD에서 발생되는 발산으로 인한 노이즈를 줄이는 역할을 수행할 수 있습니다.
기존의 SGD와 비교하여 어떠한 양상의 차이가 존재하는지 시각화하여 알아보도록 하겠습니다.
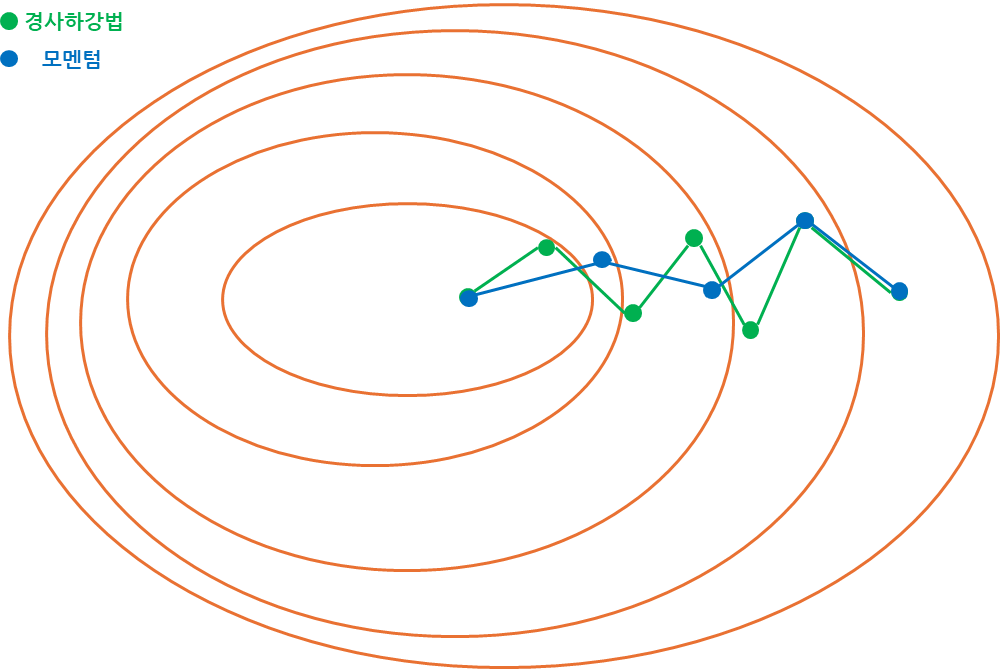
SGD에 비해 이전 가중치가 반영되어 발산이 줄어들고 더 멀리 가고 있는 것이 확인됩니다.
그렇다면 SGD와 수식을 이용하여 가중치를 갱신하는 형식이 어떻게 바뀌었는지 알아보겠습니다.
먼저 SGD로 w(가중치)를 구할 때 기존 w에서 J(손실함수)를 w로 편미분한 값을 빼게 됩니다.
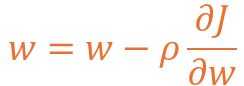
모멘텀은 기존의 방향 정보를 반영하기 위해 v라는 값을 먼저 계산하도록 유도하게 됩니다.v에는 기존 가중치의 반영 정도를 위한 a 값이 있고 해당 값은 0~1 사이의 실수 값입니다.
이렇게 계산된 v 값을 기존 가중치인 w에 반영하는 형식으로 가중치 갱신이 이뤄집니다.
일반적으로 a 값의 경우 0.5 또는 0.9 등의 값이 사용되는 점도 참고해주시면 좋습니다.
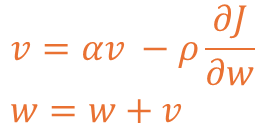
이를 TensorFlow에서 Optimizer로 사용하는 방법은 아래와 같이 작성하면 됩니다.
from tensorflow.keras.optimizers import SGD
model.compile(loss='categorical_crossentropy', optimizer=SGD(momentum=0.9), metrics=['accuracy'])😅 모멘텀의 문제점과 네스테로프 모멘텀
모멘텀도 문제가 있는데 이전 가중치와 방향을 이용하므로 기울기가 가파른 경우관성의 크기로 인해 최저점을 지나치는 Over Shooting(발산) 문제를 야기합니다.
해당 문제점은 정규화 등을 이용해 경사를 개선할 수도 있으나 다른 방법도 존재하며,
이를 개선하기 위해 고안된 방식이 네스테로프(Nesterov) 모멘텀이라 볼 수 있습니다.
네스테로프 모멘텀은 다음 가중치를 예측한 뒤 현재 가중치에 반영하는 방식입니다.가중치가 반영되는 모양을 시각화하여 나타내게 된다면 아래와 같이 나타낼 수 있습니다.
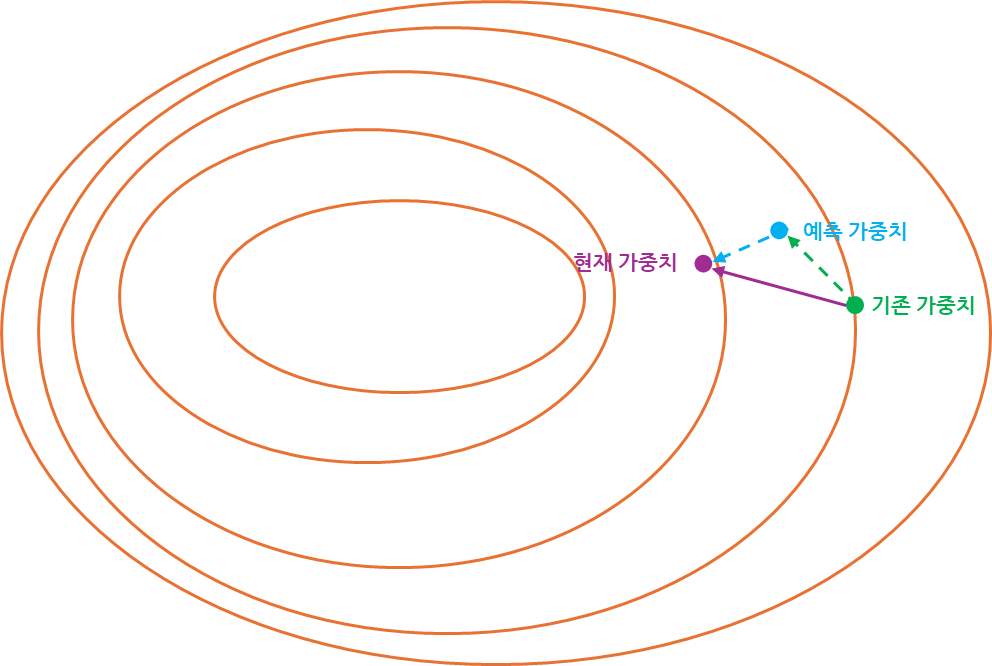
그림을 보면 예측 가중치가 존재하는데 이전 갱신된 가중치를 이용해 예측한 것으로,
예측 값을 통해 현재 가중치 값을 갱신하고 이동하는 방식으로 구성된다 볼 수 있습니다.
이러한 방식을 수식으로 나타내면 아래와 같이 3개의 수식으로 구성되는 것이 확인됩니다.
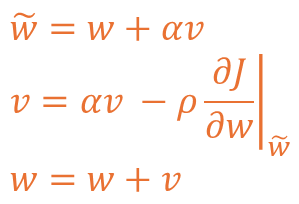
처음 계산하게 되는 ̃w는 기존 가중치에 기존 가중치에 대한 관성을 반영한 것이며,
계산된 ̃w 값을 모멘텀과 같이 갱신 후 관성을 더해 v라는 갱신 가중치를 만듭니다.
이렇게 계산된 값을 w에 반영하여 예측 가중치를 이용해 현재 가중치를 도출합니다.
이를 TensorFlow에서 Optimizer로 사용하는 방법은 아래와 같이 작성하면 됩니다.
from tensorflow.keras.optimizers import SGD
model.compile(loss='categorical_crossentropy', optimizer=SGD(momentum=0.9, nesterov=True), metrics=['accuracy'])이러한 모멘텀에 대한 방식도 존재하지만 이를 개선하기 위한 다른 방법도 존재합니다.
다음 포스팅에서는 다른 방법 중 하나인 적응적 학습률 내용을 포스팅할 예정입니다.
끝까지 읽어주셔서 감사드립니다. 😎