[Artificial Intelligence] 딥러닝에서 사용되는 규제 기법

Chance1분 미만

📲 규제 기법

딥러닝의 경우 층이 깊지 않더라도 최적화가 필요한 파라미터가 굉장히 많습니다.

이 경우 비교적 깊지 않더라도 과대적합에 빠질 수 있다는 문제가 존재하고 있지만,
딥러닝에선 보통 깊이를 줄이지 않고 과대적합을 방지하는 규제를 사용합니다.

대표적으로 데이터 증대, 드롭아웃, 가중치 감쇠가 있고 이에 대해 알아봅니다.

🪣 데이터 증대

일반적으로 데이터가 많아지게 되면 과대적합 문제의 경우 해소되는 경우가 많습니다.
하지만 새로운 데이터를 늘리는 데에는 많은 시간과 비용이 발생되는 문제점이 있습니다.

이때 인위적으로 데이터를 늘리는 규제 기법을 사용하는데 이를 데이터 증대라 합니다.
일반적으로 이미지, 영상 데이터에서 이뤄지며 방법은 아래와 같은 방법들이 존재합니다.

상하좌우로 이동
상하좌우로 회전
상하좌우로 반전
명암 조절
블러 조절
채도 조절

위 방법들을 수동으로 수행하기에는 아무래도 굉장히 많은 시간이 소요될 수 있습니다.
TensorFlow에서는 간단하게 증대하도록 ImageDataGenrator 함수를 제공합니다.

함수는 아래와 같이 선언하여 간단하게 데이터 증대기를 생성하여 이용할 수 있습니다.

from tensorflow.keras.preprocessing.image import ImageDataGenerator

bs = 6 # 한 번에 생성하는 이미지 개수

generator = ImageDataGenerator(rotation_range=30.0, width_shift_range=0.2, height_shift_range=0.2, horizontal_flip=True)
gen = generator.flow(<이미지 데이터>, <이미지 라벨>, batch_size=bs)

# 이미지와 라벨을 규칙에 맞춰 생성
img, label = next(gen)

위 함수를 이용하여 영상 데이터 셋 중 CIFAR-10 데이터를 이용한 테스트 진행 시
원본 12개의 이미지를 6개씩 2회 증대하였을 때 아래와 같은 결과가 확인됐습니다.

이러한 데이터 증대 과정에서 많이 사용되는 파라미터에 대해서도 알아보겠습니다.

rescale: 픽셀의 값을 줄이거나 늘립니다. (n/n 형태로 나누기를 위함)
width_shift_range: 1보다 작은 값일 경우 비율을 통해 이미지를 좌우로 이동합니다.
height_shift_range: 1보다 작은 값일 경우 비율을 통해 이미지를 상하로 이동합니다.
rotation_range: 파라미터의 각도만큼 이미지를 회전시킨 이미지를 제공합니다.
zoom_range: 파라미터의 수만큼 배율을 적용한 이미지를 제공합니다.
validation_split: 파라미터의 비율만큼 검증 데이터로 분리합니다.
horizontal_flip: 좌우 뒤집기 여부를 결정합니다.
vertical_flip: 상하 뒤집기 여부를 결정합니다.
fill_mode: 비어있는 픽셀이 있는 경우 채우는 방법을 결정합니다.
- neareast, constant, reflect, wrap 등

🌠 드롭아웃

너무 많은 노드를 가진 경우 드롭아웃을 통해 노드의 연결을 느슨하게 만들게 됐을 때,
성능의 큰 문제가 없거나 오히려 성능이 좋아지는 경우가 있다라는 개념에서 시작됐습니다.

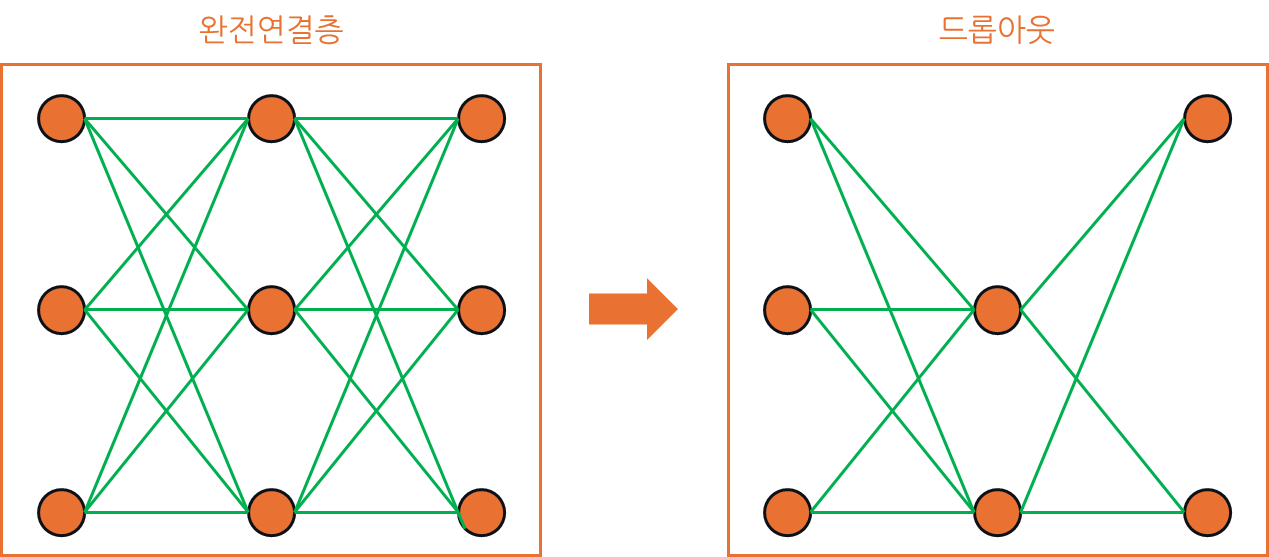
드롭아웃은 일정 비율의 노드를 임의 지정하여 사용이 불능하도록 만드는 아이디어입니다.
드롭아웃은 25%, 50% 등의 비율을 사용하고 일반적으로 50% 이상은 설정하지 않습니다.

이러한 개념을 그림으로 표현하면 완전연결층이 드롭아웃되면서 노드가 불능되면서
그와 연결됐던 에지가 모두 끊어져 신경망이 성글해진 것을 확인하실 수 있습니다.

TensorFlow에서 모델을 설계할 때 아래와 같이 추가할 경우 드롭아웃이 구현됩니다.
아래와 같이 생성 시 컨볼루션 2층 수행 및 풀링 수행 후 드롭아웃이 진행됩니다.

cnn=Sequential()
cnn.add(Conv2D(32, (3,3), activation='relu', input_shape=(32,32,3)))
cnn.add(Conv2D(32, (3,3), activation='relu'))
cnn.add(MaxPooling2D(pool_size(2,2)))
cnn.add(Dropout(0.25))
...

⬇️ 가중치 감쇠

다항식 모델은 가중치 값이 수천~수만을 넘고 이는 과대적합의 원인이 되기도 합니다.
가중치 감쇠는 모델의 오류 최소화와 동시에 가중치 값을 작게 유지하는 기법입니다.

가중치 감쇠는 두 가지 종류로 나뉘며 L1 규제(Lasso), L2 규제(Reige)라 합니다.

😎 L1 규제

L1 규제의 경우 원본 값에 가중치 절대 값의 합을 더하는 형태로 구현되는 구조이며,
일부 가중치를 0으로 만듦으로 희소성을 유도하며 중요 특징만을 선택하게 만듭니다.

이를 수식으로 표현하면 아래처럼 기존의 MSE 함수에 L1 규제를 표현할 수 있습니다.
여기서 λ는 강도를 조절하는 하이퍼 파라미터로 사용되는 요소니 참고하시면 됩니다.

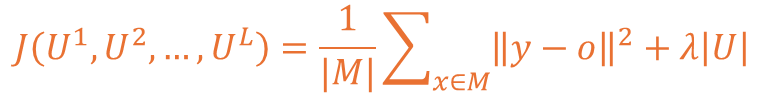
해당 수식에서 λ|U|를 풀어서 수식에 표현하게 된다면 아래와 같이 표현될 수 있습니다.
여기서 결국 안쪽에 위치하는 내용은 각 에지에 대한 가중치를 의미한다 볼 수 있습니다.

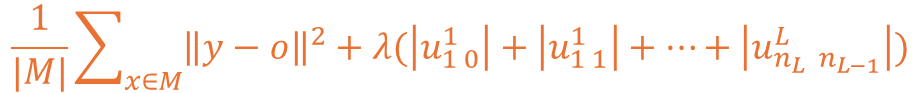
🫠 L2 규제

L2 규제의 경우 원본 값에 가중치 제곱 합을 더하는 형태로 구현되는 구조입니다.
가중치가 큰 값을 가지지 못하도록 하여 복잡도를 줄이는 효과를 갖게하는 방식입니다.

L1 규제가 희소성을 유도하는 특성이 있다면 여기서는 크기 조정 효과를 갖게 됩니다.
이를 수식으로 표현하게 될 경우 L1 규제에서 2차 Norm으로 변경된 형태로 확인됩니다.

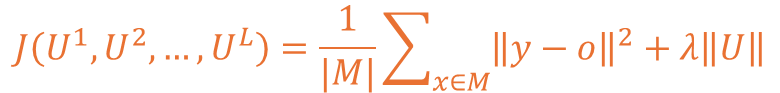
해당 수식을 풀어볼 경우 아래와 같이 가중치마다 제곱을 수행하는게 확인 가능합니다.

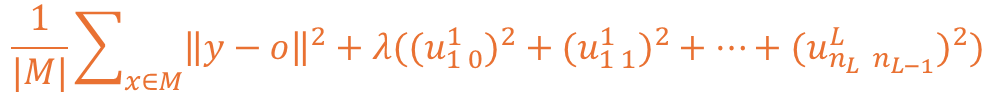
🤔 적용

해당 가중치 감쇠는 TensorFlow에서 대상에 따라 매개변수로 적용할 수 있습니다.
적용 가능한 대상은 아래와 같으며, 각각에 어떤 규제를 적용할지 아래처럼 확인됩니다.

kernel_regularizer(가중치)
bias_regularizer(바이어스)
activity_regularizer(활성 함수 결과)

from tensorflow.keras import regularizers

model.add(Dense(64, input_dim=64, kernel_regularizer=regularizer.l2(0.01), activity_regularizer=regularizer.l1(0.01)))

끝까지 읽어주셔서 감사드립니다. 😎