[Artificial Intelligence] 모멘텀과 적응적 학습률을 더한 Adam

Chance약 2 분

😀 Adam(Adaptive Momemtum Estimation)

Adam(Adaptive Momemtum Estimation)은 소개한 Momentum과 RMSProp의 결합 버전으로
현재 기준으로 딥러닝의 Optimizer 중 가장 많이 사용되고 있는 알고리즘이라 볼 수 있습니다.

🤔 개념

모멘텀을 이용하여 이전 가중치에 대한 관성을 적용하여 발산을 축소하도록 하고
여기에 적응적 학습률을 적용하여 각 매개변수 별 학습률을 적용하도록 합니다.

이때 모멘텀에서 사용하는 계수 값과 가중 이동 평균 계수를 각각 제공합니다.

이를 알고리즘과 수식을 이용하여 표현할 경우 아래와 같이 정리가 가능합니다.

기존 RMSProp 알고리즘과 비교하여 6~10번의 알고리즘에 차이가 존재하고 있습니다.
만약 RMSProp 알고리즘에 대한 해석이 필요한 경우 이전 포스팅을 참고 부탁드립니다.

⚽ 모멘텀 과정

6번과 7번의 경우 모멘텀의 계수를 반영하여 관성을 반영하는 요소로 볼 수 있습니다.

6번은 기존 v(모멘텀 벡터)에 a₁(모멘텀 계수)를 곱하여 이전 값을 축소시키고
현재의 기울기에 (1-a₁)를 곱하기 연산 후 기존 v에서 빼어 v 값을 갱신합니다.

7번은 모멘텀 벡터의 값을 보정하기 위한 요소로 v의 초기 값이 0이므로 진행합니다.
여기서는 1-(a₁)ᵗ 값으로 v 값을 나누어 학습 초기 발생되는 편향을 보정하게 됩니다.

t는 시간 스텝이라 표현하여 t가 늘어날수록 1-(a₁)ᵗ 값은 1에 수렴하게 됩니다.

😀 적응적 학습률 과정

8번과 9번의 경우 적응적 학습률을 이용하여 각각의 학습률을 도출하는 절차입니다.

8번은 RMSProp과 같이 a₂(가중 이동 평균 계수) 값을 곱하여 이전 r 값을 축소시키고
기울기 제곱에 (1-a₂)를 곱하여 연산 후 축소된 r 값에서 빼어 현재 r 값을 도출합니다.

9번은 도출된 값을 모멘텀 과정의 7번과 같이 학습 초기의 편향을 보정하는 역할을 합니다.

💡 가중치 갱신 과정

가중치 갱신을 위해 𝜌(학습률)에 모멘텀 과정에서 도출된 v 값을 곱하여 계산한 뒤,
이를 적응적 학습률 과정에서 도출된 r의 제곱근으로 나누어 갱신 가중치를 구합니다.

구해진 갱신 가중치 값을 최종적으로 기존 가중치에 반영하는 것을 반복하도록 합니다.

이렇듯 Adam의 경우 모멘텀과 RMSProp을 조합하여 학습 성능이 향상되는 효과를 봅니다.

📈 알고리즘 간 성능 비교

알고리즘 간 성능 비교로 잘 알려진 자료는 스탠포드 대학 CS231N 연구실의
Neural Network에 대한 기초 자료로 각 알고리즘 별 성능을 표현하고 있습니다.

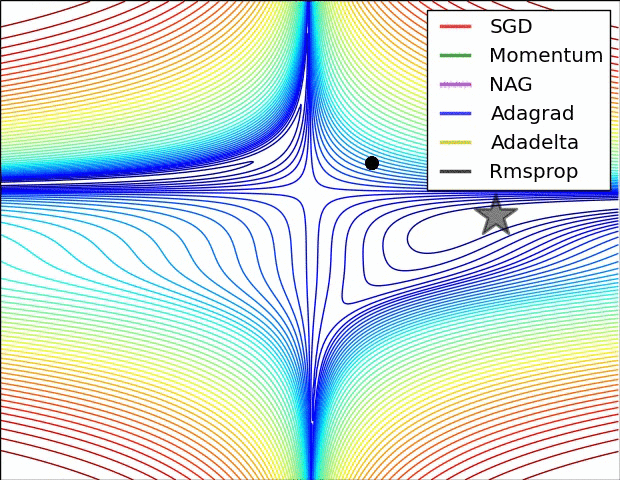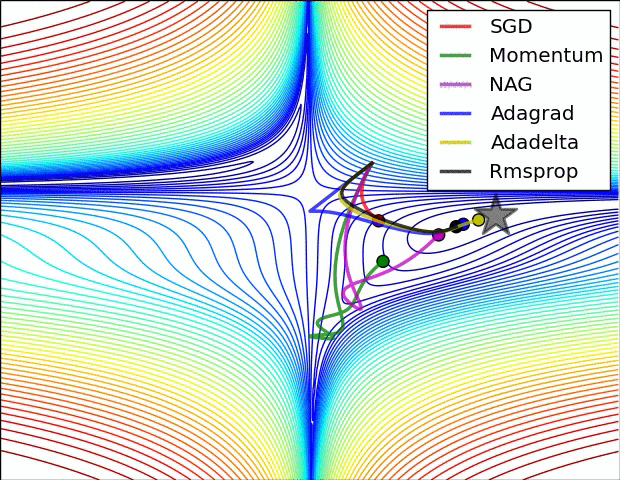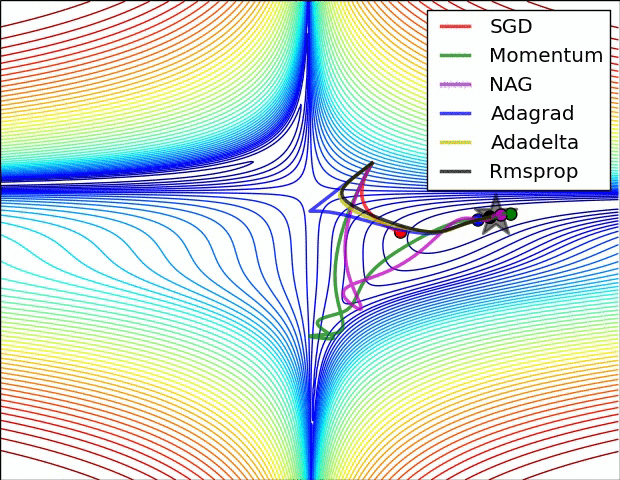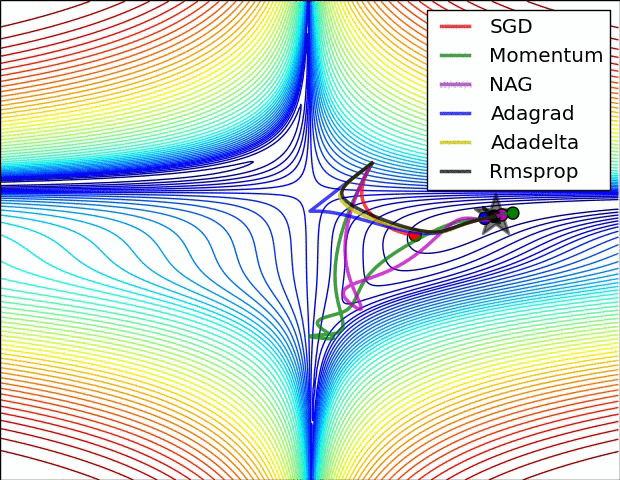
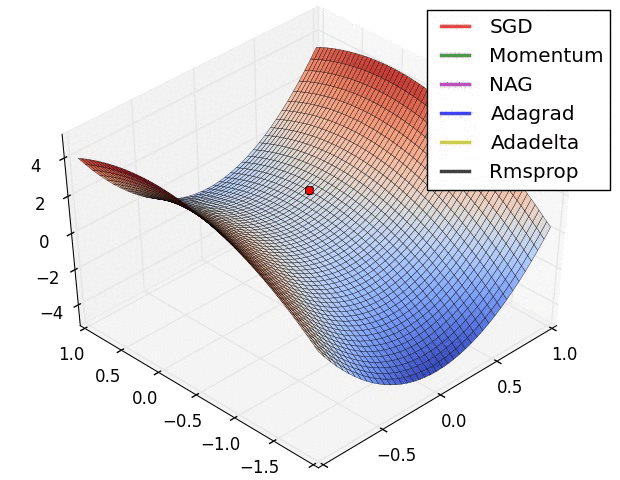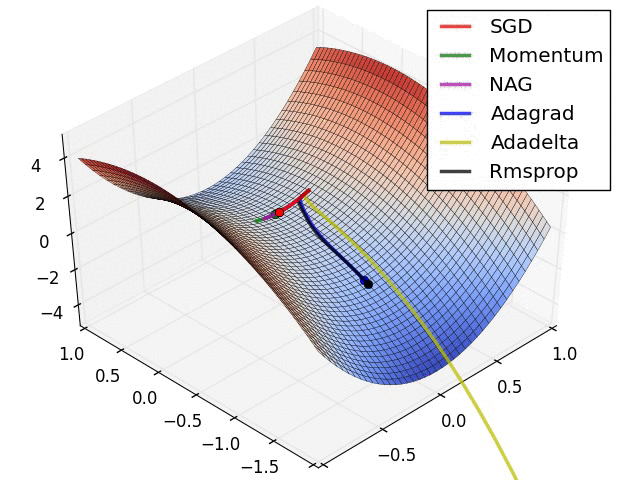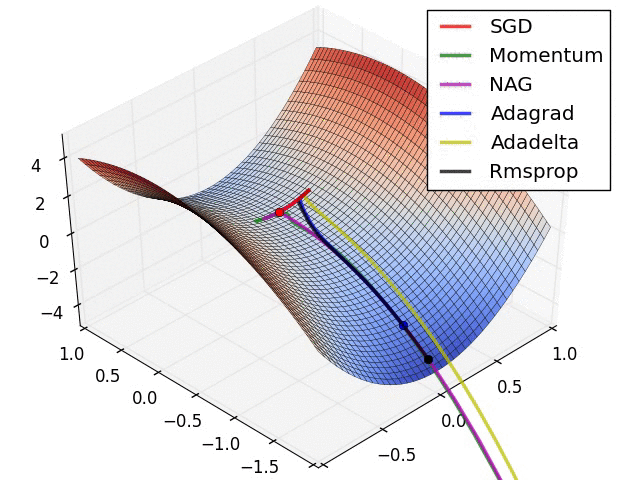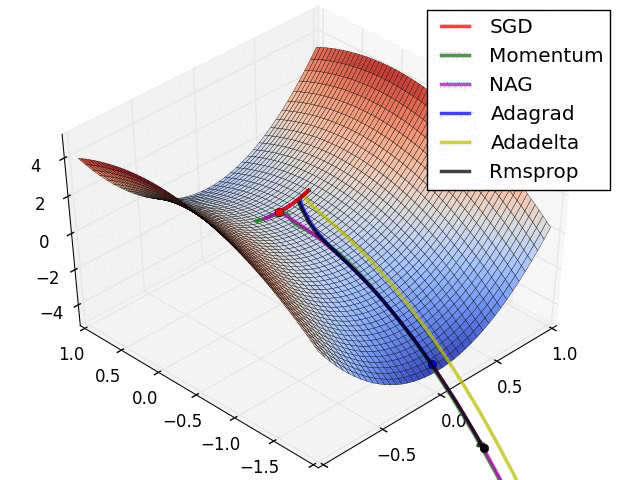
집중할 사항은 모멘텀과 NAG(네스테로프) 방식의 경우 심하게 OverShooting합니다.
또한 이미지 상 표현되는 것으로는 SGD는 학습에 어려움을 겪고 있는 것이 확인됩니다.

이에 따라 적절한 Optimizer 알고리즘을 찾아 학습하는 것이 중요하다는 것을 보입니다.

여기에는 Adam의 성능 지표는 따로 표현되지 않았기에 이를 한 번 살펴보고자 합니다.

🧑‍💻 소스 코드

해당 소스 코드는 Fastion MNIST 데이터를 이용하여 분류를 수행하는 소스 코드입니다.
인기가 있는 오일석 교수님의 파이썬으로 만드는 인공지능 책을 기반으로 작성됐습니다.

import numpy as np
import tensorflow as tf
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD,Adam,Adagrad,RMSprop

# fashion MNIST 읽어 와서 신경망에 입력할 형태로 변환
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
x_train = x_train.reshape(60000,784)
x_test = x_test.reshape(10000,784)
x_train=x_train.astype(np.float32)/255.0
x_test=x_test.astype(np.float32)/255.0
y_train=tf.keras.utils.to_categorical(y_train,10)
y_test=tf.keras.utils.to_categorical(y_test,10)

# 신경망 구조 설정
n_input=784
n_hidden1=1024
n_hidden2=512
n_hidden3=512
n_hidden4=512
n_output=10

# 하이퍼 매개변수 설정
batch_siz=256
n_epoch=50

# 모델을 설계해주는 함수(모델을 나타내는 객체 model을 반환)
def build_model():
    model=Sequential()
    model.add(Dense(units=n_hidden1,activation='relu',input_shape=(n_input,)))
    model.add(Dense(units=n_hidden2,activation='relu'))
    model.add(Dense(units=n_hidden3,activation='relu'))
    model.add(Dense(units=n_hidden4,activation='relu'))
    model.add(Dense(units=n_output,activation='softmax'))
    return model

# SGD 옵티마이저를 사용하는 모델
dmlp_sgd=build_model()
dmlp_sgd.compile(loss='categorical_crossentropy',optimizer=SGD(),metrics=['accuracy'])
hist_sgd=dmlp_sgd.fit(x_train,y_train,batch_size=batch_siz,epochs=n_epoch,validation_data=(x_test,y_test),verbose=2)

# Adagrad 옵티마이저를 사용하는 모델
dmlp_adagrad=build_model()
dmlp_adagrad.compile(loss='categorical_crossentropy',optimizer=Adagrad(),metrics=['accuracy'])
hist_adagrad=dmlp_adagrad.fit(x_train,y_train,batch_size=batch_siz,epochs=n_epoch,validation_data=(x_test,y_test),verbose=2)

# RMSprop 옵티마이저를 사용하는 모델
dmlp_rmsprop=build_model()
dmlp_rmsprop.compile(loss='categorical_crossentropy',optimizer=RMSprop(),metrics=['accuracy'])
hist_rmsprop=dmlp_rmsprop.fit(x_train,y_train,batch_size=batch_siz,epochs=n_epoch,validation_data=(x_test,y_test),verbose=2)

# Adam 옵티마이저를 사용하는 모델
dmlp_adam=build_model()
dmlp_adam.compile(loss='categorical_crossentropy',optimizer=Adam(),metrics=['accuracy'])
hist_adam=dmlp_adam.fit(x_train,y_train,batch_size=batch_siz,epochs=n_epoch,validation_data=(x_test,y_test),verbose=2)

# 네 모델의 정확률을 출력
print("SGD 정확률은",dmlp_sgd.evaluate(x_test,y_test,verbose=0)[1]*100)
print("Adagrad 정확률은",dmlp_adagrad.evaluate(x_test,y_test,verbose=0)[1]*100)
print("RMSprop 정확률은",dmlp_rmsprop.evaluate(x_test,y_test,verbose=0)[1]*100)
print("Adam 정확률은",dmlp_adam.evaluate(x_test,y_test,verbose=0)[1]*100)

import matplotlib.pyplot as plt

# 네 모델의 정확률을 하나의 그래프에서 비교
plt.plot(hist_sgd.history['accuracy'],'r')
plt.plot(hist_sgd.history['val_accuracy'],'r--')
plt.plot(hist_adam.history['accuracy'],'g')
plt.plot(hist_adam.history['val_accuracy'],'g--')
plt.plot(hist_adagrad.history['accuracy'],'b')
plt.plot(hist_adagrad.history['val_accuracy'],'b--')
plt.plot(hist_rmsprop.history['accuracy'],'m')
plt.plot(hist_rmsprop.history['val_accuracy'],'m--')
plt.title('Model accuracy comparison between optimizers')
plt.ylim((0.6,1.0))
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train_sgd','Val_sgd','Train_adam','Val_adam','Train_adagrad','Val_adagrad','Train_rmsprop','Val_rmsprop'], loc='best')
plt.grid()
plt.show()

🤔 비교 확인

정확률은 실행하는 사람마다 차이가 있겠지만 제 경우 아래와 같은 결과가 확인됩니다.

Epoch 48/50
235/235 - 20s - 84ms/step - accuracy: 0.9783 - loss: 0.0565 - val_accuracy: 0.8939 - val_loss: 0.6281
Epoch 49/50
235/235 - 21s - 90ms/step - accuracy: 0.9787 - loss: 0.0578 - val_accuracy: 0.8924 - val_loss: 0.6286
Epoch 50/50
235/235 - 20s - 84ms/step - accuracy: 0.9790 - loss: 0.0556 - val_accuracy: 0.8904 - val_loss: 0.6299

SGD 정확률은 87.41999864578247
Adagrad 정확률은 85.28000116348267
RMSprop 정확률은 88.3899986743927
Adam 정확률은 89.03999924659729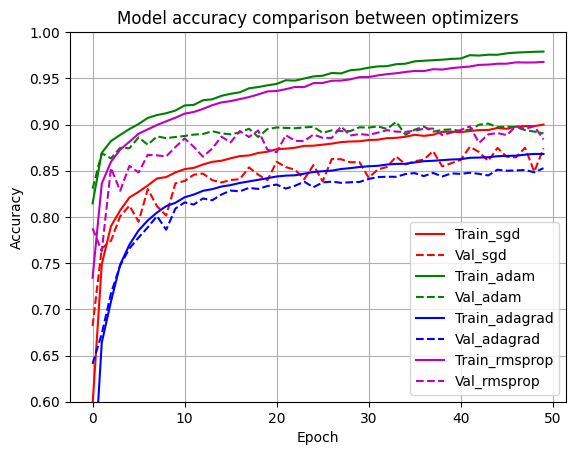

다른 알고리즘에 비해 RMSProp과 Adam 알고리즘이 높은 성능을 보이고 있는게 보이며,
의외의 결과이지만 SGD에 비해 AdaGrad 알고리즘의 정확률이 떨어지고 있습니다.

아무래도 해당 문제는 이전 언급한 그레이디언트 비중으로 인한 것으로 추측됩니다.

이렇게 경사하강법부터 시작하여 Adam 알고리즘까지의 Optimizer를 알아봤습니다.

기계학습의 성능을 향상시키기 위해 상당히 다양한 연구를 진행한 것을 확인할 수 있고
이를 통해 발전되는 과정과 최근 많이 사용되는 Adam이 어떤 구조인지 알 수 있었습니다.

저도 이런저런 공부를 하며 작성한 내용으로 틀린 내용이 있을 수 있습니다.
혹시나 틀린 내용이 있다면 댓글 부탁드리겠습니다.

끝까지 읽어주셔서 감사드립니다. 😎