[Artificial Intelligence] 학습률을 조정하는 적응적 학습률

Chance1분 미만

😀 적응적 학습률(Adaptive learning rate)의 개념

경사하강법에서 소개한 내용을 토대로 확인 시 𝜌(rho)라 불리는 학습률 값의 경우
가중치 갱신 과정에서 모두 동일한 값을 이용하여 수행된다는 것을 확인할 수 있습니다.

이를 동일 값을 사용하는 것이 아닌 각 매개변수 별 다른 값을 이용하는 것이 고안됐고,
이러한 방법을 적응적 학습률(Adaptive learning rate)이라 표현하고 있습니다.

적응적 학습률의 개념을 처음으로 도입한 Optimizer로 볼 수 있는 알고리즘입니다.
이전 그레이디언트(기울기)를 누적한 벡터를 이용하여 학습률을 적응적으로 설정합니다.

방식을 간단하게 보자면 학습률이 매개변수가 업데이트됨에 따라 반비례로 작아집니다.

매개변수 별 모두 다른 값을 이용하기에 갱신된 값이 큰 요소의 경우 작은 학습률을 갖고
반대로 갱신된 값이 작은 요소의 경우 반대로 큰 학습률을 갖게하는 방식으로 동작합니다.

이를 통해 학습이 진행되는 과정에서 가중치 갱신 간 학습률이 적응적으로 변동됩니다.

AdaGrad는 아래와 같은 알고리즘과 수식을 이용해 동작되는 것을 확인할 수 있습니다.

알고리즘을 간단하게 리뷰하면 𝜌(학습률)을 이용하여 손실의 기울기를 구하고
각 요소 별 기울기의 제곱 값을 구하고 기존의 r(누적 벡터) 값에 덧셈 연산합니다.

구해진 r 값의 제곱근을 분모로 두고 𝜌와 각 기울기를 곱한 값을 분자로 두어
각 매개변수 별 갱신할 가중치 값을 도출한 뒤 반영하는 것을 반복하는 구조입니다.
(여기서 𝜖는 분모가 0에 수렴되지 않도록 하기 위함으로 매우 작은 값으로 구성)

알고리즘 상에 표기된 5~7번의 경우 수식을 풀어볼 경우 아래와 같이 구성됩니다.

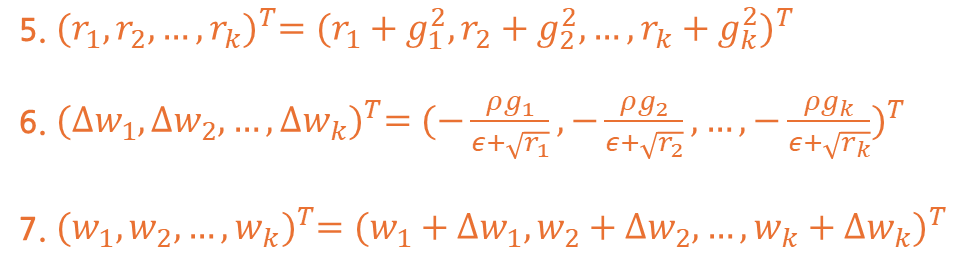
5번 수식의 경우 각 요소 별 기존 r 값에 g의 제곱의 합을 구하는 것을 의미합니다.

6번 수식은 𝜌와 기울기를 곱한 값을 r 제곱근으로 나누어 갱신 가중치를 구합니다.
6번 수식에서 기울기 합에 따라 학습률 값이 변동되어 적용됨을 확인할 수 있습니다.

마지막으로 7번 수식은 가중치에 갱신 가중치를 더하여 다음 가중치를 구한 것입니다.

AdaGrad는 초기 학습에서는 좋은 성능을 보이지만 학습이 진행될수록 문제가 있습니다.
여기서 발생되는 문제는 보통 2가지 정도로 나뉠 수 있으며 아래와 같이 정리 가능합니다.

AdaGrad의 단점인 학습 지연 문제와 그레이디언트의 비중 역할 문제 해소를 위해
이전 그레이디언트를 누적할 때 오래된 것의 영향을 줄이는 정책을 적용한 방법입니다.

RMSProp에서는 a라는 값을 이용하여 가중 이동 평균 기법을 방법이라 볼 수 있습니다.

동작하는 방식의 알고리즘은 아래과 같이 구성되고 수식은 AdaGrad와 거의 동일합니다.

알고리즘 상 5번 부분에 존재하지 않던 a 값이 위치한 것을 확인할 수 있습니다.
a 값이 작을수록 최신 그레이디언트에 비중을 두어 가중치 갱신을 수행합니다.

일반적으로 0.9, 0.99, 0.999 값을 사용하는 것으로 알려져 있습니다.

변경된 수식인 5번에 대한 내용만 수식으로 따로 정리해보면 아래와 같습니다.

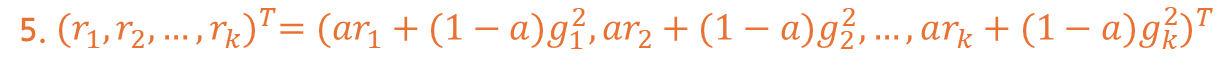
위와 같이 동작하게 된다면 기존의 기울기 벡터는 학습 과정에서 점점 작아집니다.
또한 값이 커져서 발생되는 문제도 기울기를 더할 때 값을 축소하기에 약화됩니다.

AdaGrad에 대한 한계를 어느정도 극복하여 만들어진 RMSProp도 문제점은 존재합니다.
문제는 아래처럼 총 3가지 정도로 정리되오니 참고하시어 이용해주시면 될 것 같습니다.

위와 같은 문제로 인해 Adam이라는 Optimizer가 고안됐고 다음 포스팅으로 소개하겠습니다.

끝까지 읽어주셔서 감사드립니다. 😎