[Artificial Intelligence] 확률분포의 차이를 계산하는 KL-Divergence

📈 KL(Kullback-Leibler) Divergence

이전 포스팅을 통해 불확실성을 측정하기 위한 엔트로피에 대한 개념을 알아봤습니다.

KL-Divergence는 교차 엔트로피를 이용하여 확률분포의 차이를 계산하는 함수로
근사하는 다른 분포를 샘플링 시 발생할 수 있는 정보 엔트로피의 차이를 계산합니다.

여기서 계산된 것을 상대 엔트로피, 정보 획득량, 인포메이션 다이버전스라 합니다.

Divergence는 발산을 의미하기 때문에 분포에 대한 발산 정도로도 볼 수 있습니다.

🔢 수식 유도

KL-Divergence의 경우 수식을 통해 유도할 수 있는데 먼저 수식을 알아보겠습니다.

KL-Divergence 수식 유도

수식은 교차 엔트로피의 기본 수식으로부터 유도되고 과정은 다음과 같다고 볼 수 있습니다.

1. 교차 엔트로피 수식에 +- 값으로 엔트로피 관련 수식을 작성합니다.
2. 엔트로피 계산 간 사용되는 수식인 - 값이 존재하는 수식을 H(P)로 대체합니다.
3. 교차 엔트로피 수식과 남은 수식을 +, - 순서로 정렬하고 이를 요약합니다.
4. 양 변에 -H(P)를 추가하여 우변에 존재하는 H(P) 값을 제거합니다.
5. H(P,Q)-H(P)에 대한 수식이 유도됐고 해당 값이 KL-Divergence 입니다.

😲 수식 표현

KL-Divergence는 수식 표현 간 KL(P||Q)라 표현하고 아래처럼 수식 표현이 가능합니다.

KL-Divergence 수식

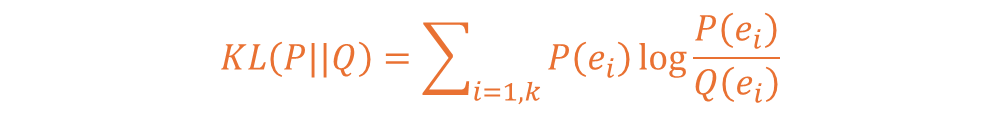
🤔 사용 용도

일반적으로 교차 엔트로피의 값을 작게 만들어 H(P)(실제 값)과 근접하게 만드는 것은
다른 의미로는 H(P) 값은 고정된 값이므로 KL-Divergence의 값을 줄이는 것과 같습니다.

😏 특성

KL-Divergence는 2가지의 특성이 대표적으로 특성은 아래와 같습니다.

1. KL(P||Q)의 값은 항상 0이상의 값을 갖습니다.
2. KL(P||Q)와 KL(Q||P)의 값을 같지 않고 거리의 개념이 아닙니다.

1번 특성의 경우 H(P, Q)의 값은 항상 H(P)보다 크기 때문에 성립됩니다.

2번 특성의 경우 H(P, Q) != H(Q, P), H(P) != H(Q)라는 특성과 연관됩니다.
해당 값이 다르기 때문에 KL(P, Q) != KL(Q, P)라는 특성이 성립되게 됩니다.

해당 부분은 유클리디안 거리 등과 달리 거리의 개념이 아님을 반증하고 있습니다.

---

끝까지 읽어주셔서 감사드립니다. 😎