[Artificial Intelligence] 불확실성을 측정하는 교차 엔트로피
📀 교차 엔트로피 (Cross Entropy)
교차 엔트로피는 인공지능의 분류(Classification) 문제에서 많이 사용되는 함수입니다.
이 함수가 무엇이고 어떠한 역할을 하기에 많이 사용되고 있는지 알아보도록 하겠습니다.
💿 엔트로피 (Entropy)
교차 엔트로피를 이해하기 위해서는 먼저 엔트로피에 대한 개념을 이해해야 합니다.엔트로피는 간단하게 말하면 확률의 분포에 따른 불확실성을 측정하는 함수입니다.
예를 들어 어느 하나의 확률이 높지 않은 공정한 6면 주사위가 있다는 가정을 합니다.
이 경우 1부터 6의 모든 숫자가 모두 같은 1/6의 확률을 갖는다는 것을 알 수 있습니다.
만약 주사위가 찌그러져 1이 나올 확률이 1/2가 되고 다른 면의 확률이 1/10가 됐다면
1의 확률이 높다는 것을 알 수 있고 공정한 주사위보다 불확실성이 낮다 표현합니다.
📖 엔트로피의 수식
이러한 경우의 엔트로피를 각각 계산할 수 있고 기본적인 계산식은 아래와 같습니다.
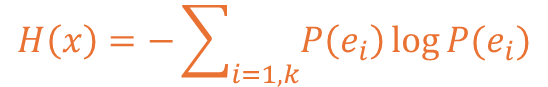
수식에서 x는 값을 제공하는 확률 변수를 의미하고 k는 사건에 대해 의미합니다.
주사위는 6개의 각기 다른 사건이 존재하므로 k의 값은 6이 된다고 볼 수 있습니다.
다음으로 i는 주사위를 기준으로는 1~6의 수가 나오는 사건을 의미할 수 있으며,P(eᵢ)는 주사위에서 i 변수의 수가 나오는 각기의 확률을 의미하고 있습니다.
여기서 log는 밑이 e인 자연로그를 이용해 계산되는 점 참고해주시면 됩니다.
추가로 log는 분자보다 분모가 작을 시 음수가 나오니 -로 양수로 변환합니다.
(확률이라는 전제이므로 100%를 초과할 수 없기에 양수가 나올 수 없습니다.)
✨ 엔트로피 계산
설명된 수식을 통해 공정한 주사위의 엔트로피를 계산하면 아래와 같습니다.
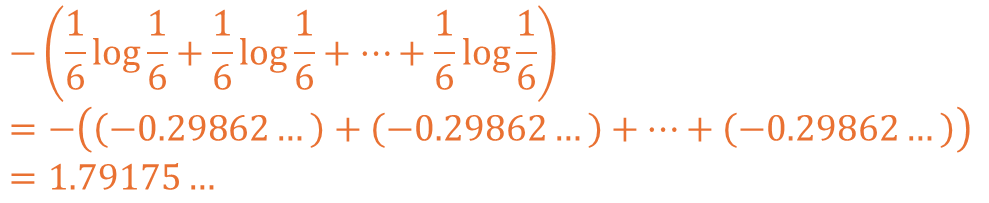
다음으로 1이 더 많이 나오는 주사위의 경우 아래와 같이 계산될 수 있습니다.
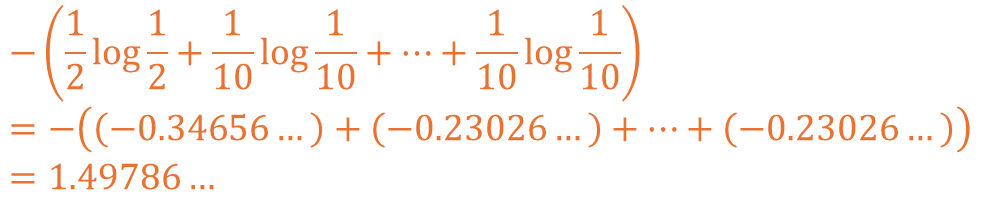
각 1.79175와 1.49786의 값이 도출되고 불확실성이 더 낮은 것이 확인됩니다.
🦾 교차 엔트로피란?
교차 엔트로피는 엔트로피를 이용해 두 확률 분포의 다른 정도를 측정하는 것입니다.
예로 동일한 공정한 주사위 두 개를 비교했을 때와 다른 주사위의 확률을 비교합니다.
이 경우 당연히 공정한 주사위 두 개를 비교한 것이 차이가 적다는 것을 알 수 있습니다.
이러한 과정을 수식으로 만들어 서로 간의 차이의 척도를 측정하는 것을 의미하고 있습니다.
📖 교차 엔트로피의 수식
교차 엔트로피의 수식은 기본적으로 엔트로피의 수식에서 사용되는 변수 값이 변경됩니다.
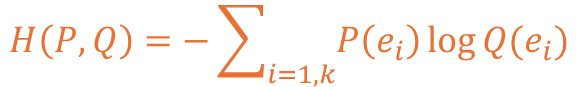
확인 시 제공되는 변수 값이 P와 Q인 것을 볼 수 있고 이는 각각의 확률 분포를 의미합니다.
나머지의 값은 마찬가지로 서로의 동일한 대상에 대한 비교를 하는 것이 목표인 것이 됩니다.
✨ 교차 엔트로피 계산
그렇다면 먼저 교차 엔트로피를 이용하여 공정한 주사위 두 개에 대해 비교해보겠습니다.
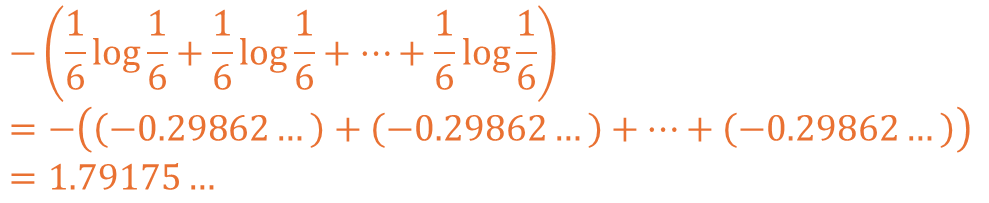
당연하게도 P, Q는 같고 처음 계산한 공정한 주사위의 엔트로피 값과 같다는 것이 확인됩니다.
그렇다면 P를 공정한 주사위로 Q를 1이 더 많이 나오는 주사위로 계산한다면 어떨까요?
이를 수식을 이용하여 계산할 경우 아래와 같이 계산되는 것을 확인하실 수 있습니다.
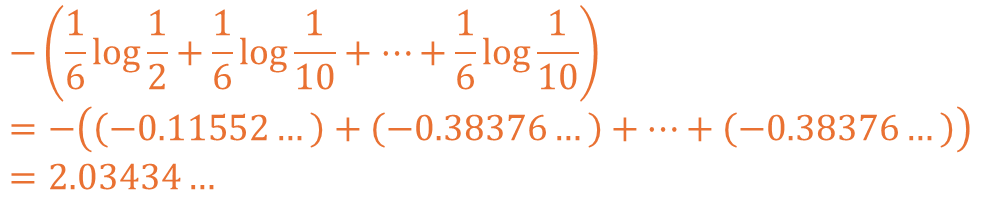
확인 시 공정한 주사위 두 개를 서로 비교했을 때보다 더 높은 불확실성을 보입니다.
이를 통해 확인 가능한 것은 두 가지의 차이에 대한 상세한 비교가 가능하다는 것입니다.
기계학습에서는 P에 정답(레이블)을 제공하고 Q에 예측을 제공하여 이용 가능합니다.
🤔 교차 엔트로피 사용 용도
그렇다면 교차 엔트로피를 왜 사용할까에 대한 의문이 들 수 있을 것이라 듭니다.
우선 MSE(Mean Squared Error)의 경우 제곱이라는 특성을 갖고 있기 때문에,
1 미만의 값은 작아지며 0에 가까워지고 1 이상의 경우 커지면서 차이가 벌어집니다.
이로 인한 불공정성 문제가 발생되고 분류 문제에서 큰 걸림돌이 될 수 있습니다.
교차 엔트로피는 이러한 부분을 확률 분포의 불확실성을 측정하는 형태로 제공하여MSE에서 발생될 수 있는 불공정성의 문제를 해소하고 학습 성능을 높일 수 있습니다.
예를 들어 숫자 분류 과정에서 아래와 같은 결과가 도출됐을 때 계산에 대한 부분입니다.
0이 정답이고 예측이 정답인 경우와 틀린 경우를 비교할 때 아래와 같이 이뤄집니다.
| 상황 | y |
|---|---|
| 정답 | (0, 0, 0, 1, 0, 0, 0, 0, 0, 0) |
| 예측 1 (성공) | (0.9, 0, 0, 0, 0, 0, 0, 0, 0, 0.1) |
| 예측 2 (실패) | (0.1, 0, 0, 0, 0, 0, 0, 0, 0, 0.9) |
먼저 MSE를 이용하여 해당 수식을 계산하여 값을 비교해보면 아래와 같습니다.
예측 1 상황을 MSE로 계산해보면 아래와 같이 전개되고 0.002의 값이 도출됩니다.
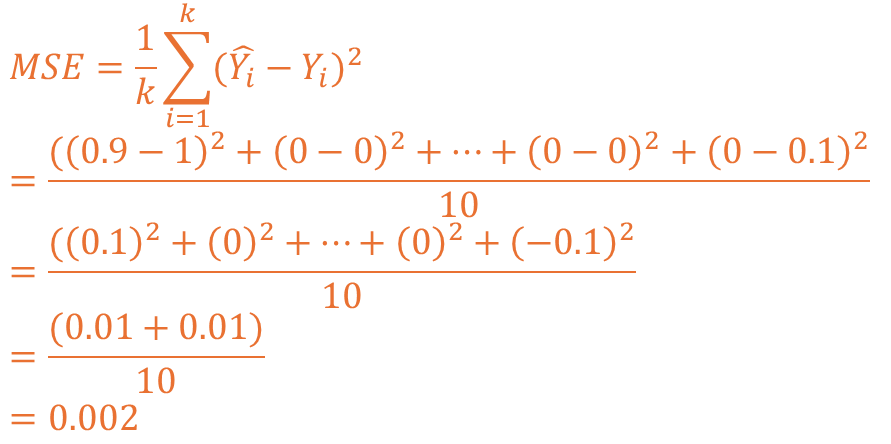
예측 2 상황을 MSE로 계산해보면 아래와 같이 전개되고 0.0162의 값이 도출됩니다.
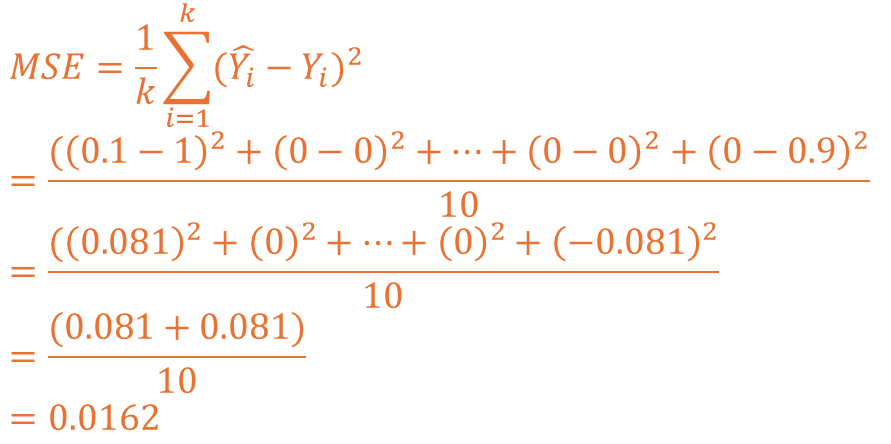
도출된 값을 보면 확률이기 때문에 0에 점점 가까워지고 있고 차이가 크지 않습니다.
만약 이를 교차 엔트로피를 이용하여 계산할 경우 아래와 같이 계산 가능합니다.
예측 1 상황을 교차 엔트로피로 계산해보면 아래와 같이 전개되고 0.1053의 값이 도출됩니다.
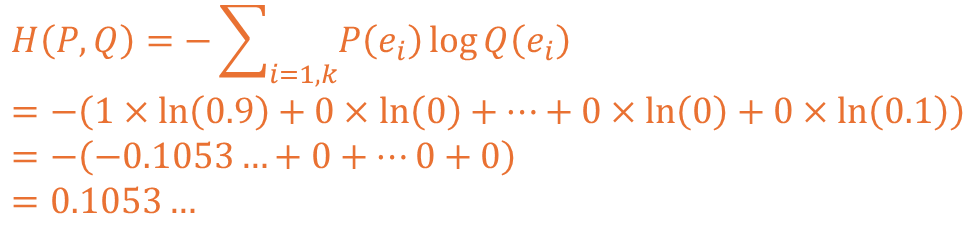
예측 2 상황을 교차 엔트로피로 계산해보면 아래와 같이 전개되고 2.3025의 값이 도출됩니다.
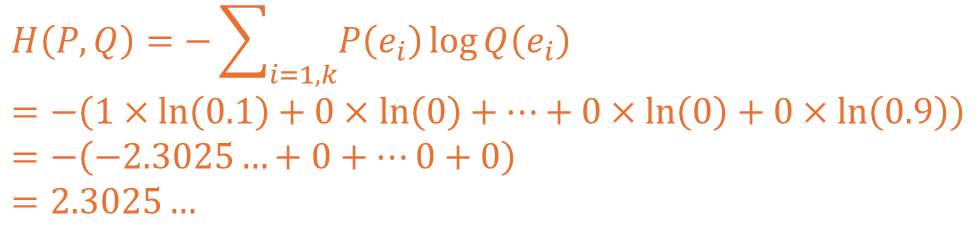
값을 비교해보면 차이가 크고 이는 MSE의 불확실성을 해소하는데 도움이 됩니다.
💡 MSE와 교차 엔트로피의 사용 용도
MSE는 위와 같은 문제로 인해 분류 문제에서는 많이 사용되지 않고 있는 상태이며,회귀 문제의 경우 확률이 아닌 값을 비교하는 형태이므로 응용하여 사용됩니다.
그러므로 분류는 교차 엔트로피, 회귀는 MSE/MAE 등을 떠올려주시면 됩니다.
끝까지 읽어주셔서 감사드립니다. 😎